30 60 90 Üçgeni Kuralı Nedir Ve Özellikleri Nelerdir?
30 60 90 üçgeni açıları 30°, 60° ve 90° olan sinüs, kosinüs tanjant ve kotanjant gibi trigonometrik fonksiyonları hesaplamak için kullanılabilen kenarları ve açıları arasında iyi tanımlanmış ilişkilere sahip olduğu için trigonometride yaygın olarak kullanılan özel bir dik üçgen türüdür.
Aynı zamanda “ikiye bölünmüş eşkenar üçgen” olarak da bilinir, çünkü bir eşkenar üçgen çizip kenarlarından birine yükseklik çizerseniz, iki adet 30-60-90 üçgeni oluşturursunuz.
30 60 90 Üçgeni Kuralı
Tüm kurallar arasında geometri 30 60 90 üçgeni kuralı önemli bir yer tutar. Çünkü, kenar uzunlukları arasında bilinmeyen değerleri çözmek için kullanılabilecek öngörülebilir oranlara sahip oldukları için geometri ve trigonometride kullanışlıdır.
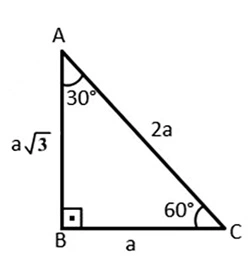
Bu üçgenin kenar uzunlukları özel bir orandadır. 30 60 90 üçgeni kenar uzunlukları aşağıdaki gibi özetlenebilecek belirli bir ilişkisi vardır.

- Hipotenüs uzunluğu 30° lik açının karşısındaki kenarın uzunluğunun iki katıdır.
- 60° lik açının karşısındaki kenar uzunluğu 30° lik açının karşısındaki kenar uzunluğunun √3 katıdır.
- Her zaman 30° lik açının karşısındaki kenar uzunluğunu hareket başlangıcı kabul edeceğiz. Çünkü küçükten büyüğe geçiş daha kolaydır.
En kısa kenar = a
Uzun kenar = a√3
Hipotenüs = 2a
İşte sadece bu oranları bilmemiz bile çözümlemeye ve pratik yapmaya olanak sağlayacaktır. Onun için bu oranları aklımızda tutalım. Bilmemiz gereken 1, √3 ve 2.
Örnek;
Bir dik üçgende 30° lik açının karşısındaki kenarın uzunluğu 6 cm ise, diğer kenarların uzunlukları kaç cm dir.
Hipotenüs, 30 derecelik açının karşısındaki kenarın uzunluğunun iki katıdır, bu nedenle 2 . 6 = 12 cm dir.
60 derecelik açının karşısındaki kenar 30 derecelik açının karşısındaki kenarın uzunluğunun (√3) katı olduğundan 6 .√3 = 6√3 cm olur. Yada hipotenüsün uzunluğunun (√3)/2 katı olduğundan yine 12 . (√3)/2 = 6√3 cm dir.
Dolayısıyla bu 30-60-90 üçgeninin kenarları 6 cm, 6√3 cm ve 12 cm dir.
30 60 90 üçgeni örneklerini çoğaltabiliriz. 30 60 90 üçgeni soruları ve cevapları üçgen testleri kategorisi altında dik ve özel üçgenler testlerinde bulabilirsiniz. bakınız.
Sonuç olarak bir kenar uzunluğunu biliyorsanız, bu oranı kullanarak diğer iki kenarın uzunluklarını da bulabilirsiniz.
Peki herhangi iki kenarın uzunluğunu biliyorsak…
Evet üçüncü kenarın uzunluğunu bulmak için yine bu oranları kullanabileceğimiz gibi bir dik üçgenin dik kenarların karelerinin toplamının hipotenüsün karesine eşit olduğunu belirten Pisagor bağıntısını da kullanabiliriz.
Oranları biliyoruz ama 30° karşısındaki mi 60° karşısındakinin √3 katıydı yoksa 60° karşısındaki mi 30° karşısındakinin √3 katıydı karıştırdık…
Ne yapacağız?
30 60 90 üçgeni çizelim.
Hemen 30° lik açının karşısındaki kenar uzunluğu en kısa kenar olduğundan 1 birim yazalım.
Sonra 2 mi büyük √3 mü sorusunu soruyoruz. √3 √4 olsa 2 değerini alırdı demek ki 2 büyük diyoruz…
2 en büyük olduğuna göre 90° lik açının karşısındaki kenara 2 birim ve dolayısıyla üçüncü kenara da yani 60° lik açının karşısındaki kenara √3 birim yazabiliriz.
Ya kuralı bilmiyorsak…
Sin(30) Değerinin 30-60-90 Üçgenindeki Önemi
Sin(30) değerinin 30-60-90 üçgenindeki kısa kenar, uzun kenar ve hipotenüs arasındaki oranları belirlemedeki önemini inceleyeceğiz. Trigonometri, geometri ve matematikte önemli bir rol oynayan bir dal olarak karşımıza çıkar. Özellikle üçgenlerde trigonometri fonksiyonlarının kullanılması, açıların ve kenar uzunluklarının birbirleriyle ilişkisini anlamamızı sağlar.
Sinüs fonksiyonu, bir açının karşısındaki kenarın hipotenüse oranını temsil eder. Sin(30) değeri 30-60-90 üçgeni gibi özel üçgenlerin analizinde ve geometrik hesaplamalarda önemli bir role sahiptir. İşte burada sin(30) devreye girer.
30° açısının sinüsünün değeri matematiksel olarak sin(30) olarak ifade edilir. 30° açısının sinüsü, 1/2 dir. Yani sin(30) = 1/2. Bu da demek oluyor ki, kısa kenar hipotenüsün yarısı kadar olacaktır.
Yani 30 60 90 üçgeninde hipotenüs uzunluğu 30° lik açının karşısındaki kenarın uzunluğunun iki katıdır.
Sonuç olarak trigonometri fonksiyonlarından sinüs değerlerinin üçgenin kenar uzunluklarındaki oranları belirlemede önemli bir rol oynadığını gösterir.
Bir 30°- 60°- 90° üçgeni çizelim.
sin30° karşı kenar bölü hipotenüs 1/2 olduğundan 30° lik açının karşısındaki kenar uzunluğuna 1 hipotenüse 2, 60° lik açının karşısındaki kenara da ya sin60° dan yada pisagor bağıntısından √3 yazarak aralarındaki oran belirleyebiliriz.
Burada 30 60 90 üçgeninde en önemlisi ya kuralı bileceğiz yada trigonometri fonksiyonunu uygulayacağız.
Ya hiçbir fikrimiz yoksa…
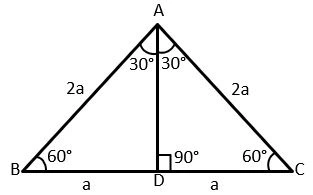
Bir eşkenar üçgende herhangi bir kenara dik iniyoruz. Dikme hem kenarortay hem açıortay hem de yükseklik olacağından kenarı iki eşit uzunluğa ayırıyor. Dolayısıyla 1′ e 2 oranını görüyoruz. Üçüncü kenarı da pisagor bağıntısını kullanarak 30 60 90 üçgeninin kenar uzunlukları birbiriyle En kısa kenar = a, Uzun kenar = a√3, Hipotenüs = 2a oranına sahip olduklarını belirleyebiliriz.
30 60 90 Üçgen: Altın Oran
30 60 90 üçgeni , yüzyıllardır sanatçılar, mimarlar ve bilim insanları tarafından sevilen bir kavram olan altın oranla bağlantılıdır . 30, 60 ve 90 derecelik açılara sahip bu üçgenin altın oranla özel bir bağı vardır . Bu oran, doğada, sanatta ve tasarımda uyum ve denge sembolü olarak görülür.
Üçgenin kenar uzunlukları benzersiz bir desen gösterir. En kısa kenar en uzun kenarın yarısıdır ve orta kenar en kısa kenarın 3 katının kareköküdür. Bu desen , güzelliği ve dengesiyle bilinen bir sayı olan altın orana (yaklaşık 1.618) bağlıdır.
30 60 90 Üçgenlerin Gerçek Dünya Örnekleri
30 60 90 üçgeninin özellikleri ve uygulamaları onu geometrik problemlerin çözümünde ve gerçek dünya yapılarının tasarımında değerli bir araç haline getirir.
Binalarda ve günlük eşyalarda bulunur. Bu, ne kadar kullanışlı ve yaygın olduğunu gösterir. Mühendislik, mimarlık ve inşaat gibi alanlarda gerçek uygulamalara sahiptir. Rampalar, merdivenler ve kademeli eğimli diğer yapıları tasarlamak ve inşa etmek için kullanılabilir.
Paris’teki Eyfel Kulesi harika bir örnektir. İskeleti, sağlamlık ve güzellik için 30 60 90 üçgen kullanır. Avustralya’daki Sidney Opera Binası da tasarımında bu üçgenleri kullanır.
Ancak bu sadece büyük binalarda geçerli değil. Kutu uçurtmalarda, güneş panellerinde ve dizüstü bilgisayar menteşelerinde 30 60 90 üçgenler görebilirsiniz. Bu öğelerin iyi çalışmasına ve uzun süre dayanmasına yardımcı olurlar.
| Gerçek Dünya Örneği | Başvuru |
|---|---|
| Eyfel Kulesi, Paris | Yapısal destek ve tasarım |
| Sidney Opera Binası, Avustralya | Çatı tasarımı ve mimarisi |
| Kutu Uçurtmalar | Uçurtmanın yapısı ve dengesi |
| Güneş Panelleri | Yansıtıcı paneller ve verimlilik |
| Dizüstü Bilgisayar Menteşeleri | Stabilite ve işlevsellik |
Bu örnekler 30 60 90 üçgeninin her yerde nasıl kullanıldığını gösteriyor. Muhteşem binalar ve kullanışlı eşyalar yaratmaya yardımcı oluyor. Özel nitelikleri birçok kişiye yeni ve ilginç şeyler yapma konusunda ilham veriyor.