GEOMETRİ FORMÜLLERİ

Göreceğiniz her soru tipi ne kadar çok olursa olsun geometri formülleri ve kurallarının kullanılması nihai cevaba etkisi ve katkısı çoktur.

Geometri sorularını çözmek; mantığı kavranılan belirli bir düzeyde bilgi, son derece dikkat isteyen ve deneyim kazanılmış bir bakış açısı gerektirir.Ki bunda geometri formülleri kullanılır.Birçok işlem gerektirecek matematik ifadeler, formüllere dökülerek soruları hızlı ve pratik yanıtlamayı mümkün kılar.

Konular birbirleriyle bağlantılı olduğundan farklı ve değişik yöntemlerle formül kullanma sonucunda problemin çözüm yolları daha rahat görülür.Bunun yanı sıra işlem hatasına düşme ihtimali azalır.

TYT-AYT Matematik testinde; daha kısa, pratik, çözüme yönelik sonuçlara ulaşmak önem kazanır.Asıl mesele öğrencinin veyahut adayın matematik testinden ne kadar çok net yapmış olduğudur.

Bunu söylerken kastettiğimiz başlı başına bir kalıp gibi “formüllerin ezberlenmesi” değildir.

Ancak problemlerde çokça rastlanılan Geometri dersinin yapı taşları pisagor bağıntısı başta olmak üzere tales, temel benzerlik, öklid, kosinüs formüllerini bilmek; pratik yapmaya olanak sağlar.

Üzerinde zaman ayırarak, kademe kademe ilerleyerek, deneyim elde etmelisiniz.Kazandığınız deneyim ister istemez sizi matematik-geometri formülleri kullanmanıza yöneltecek.Bu sayede formüllerin akılda kalıcılığını sağlamış, yani hem anlamış hem de ezberlemiş olacaksınız.

Bunu yaparken ya olabildiğince çok soru çözmelisiniz yada teoremlerin ispatını çok iyi yapabilmelisiniz

Bir sonraki kademeye ilerlediğinizde de mütemadiyen tekrar eden nokta içindeki nokta gibi hep aynı geometri temel kavramların, aksiyomların, teoremlerin kullanıldığını farkedeceksiniz.

YKS-TYT-AYT Geometri Formülleri PDF dosyasını Geometri PDF İndir sayfasından indirebilirsiniz.Geometri PDF İndir linkine sayfa sonundaki resme tıklayarak erişebilirsiniz.

Görsellerdeki geometri formüllerini inceleyiniz.

Geometri Şalvar-Bumerang-Füze-Roket Kuralı

Şekildeki gibi içbükey-konkav bir dörtgende, (üçgeninin kenarı içe büküldüğünde oluşan açının ölçüsü) x=a+b+c ile formüle edilir.

İki İç Açıortay Açı Formülü

Bir üçgende iki iç açıortayın oluşturduğu açının ölçüsü, üçüncü köşedeki iç açının ölçüsünün yarısından 90° fazladır.

İki Dış Açıortay Açı Formülü

Bir üçgende iki dış açıortayın oluşturduğu açının ölçüsü, üçüncü köşedeki açının ölçüsünün yarısının tümleridir.Diğer bir deyişle bir üçgende iki dış açıortayın oluşturduğu açı, 90°den üçüncü köşedeki açının yarısı kadar eksiktir.

İç Ve Dış Açıortay Açı Formülü

Bir üçgende komşu olmayan bir iç açı ve bir dış açının açıortaylarının oluşturduğu açının ölçüsü, üçüncü köşedeki açının ölçüsünün yarısına eşittir.

Üçgen Eşitsizliği Formülü

Bir üçgende bir kenar uzunluğu; diğer iki kenarın uzunlukları toplamından küçük, farkının mutlak değerinden büyüktür.

Şekildeki ABC üçgeninin kenar uzunlukları a, b, c ise; |b-c|<a<b+c, |a-c|<b<a+c, |a-b|<c<a+b dir.

Üçgen Eşitsizliği Çevre Formülü

Bir ABC üçgeninin içinde alınan herhangi bir noktanın, üçgenin köşelerine olan uzunlukları toplamı; üçgeninin yarı çevresinden büyük, çevresinden küçüktür.

Şekildeki ABC üçgeninde |BC|=a, |AC|=b, |AB|=c ve a+b+c=2u olmak üzere; u<|KA|+|KB|+|KC<2u dur.

Tales Teoremi Formülü

Paralel doğruları kesen herhangi iki doğru üzerinde, paralellerin ayırdıkları doğru parçaları orantılıdır.

Şekilde d1//d2//d3, m ve n doğruları kesen ise; |AB|/|BC|=|DE|/|EF|, |AB|/|AC|=|DE|/|DF| ve |BC|/|AC|=|EF|/|DF| dir.

Muhteşem Üçlü Formülü

Bir dik üçgende hipotenüse ait kenarortay hipotenüs uzunluğunun yarısına eşittir.Diğer bir deyişle bir dik üçgende hipotenüsün orta noktası köşelere eşit uzaklıktadır.

Şekildeki ABC üçgeninde, m(A)=90° ve |BD|=|DC| ise; |BD|=|DC|=|AD| dir.

Özel Açılı Üçgen Formülleri

Bir dik üçgende 30° lik açının karşısındaki kenar uzunluğu x birim ise; hipotenüs uzunluğu 2x birim, 60° lik açının karşısındaki kenar uzunluğu da xkök3 birimdir.

Bir 15°-75°-90° dik üçgeninde hipotenüse ait yükseklik, hipotenüsün dörtte biri kadardır.

Özel Üçgen Formülleri

İkizkenar üçgende taban üzerinde alınan bir noktadan eşit kenarlara indirilen dikmelerin toplamı eşit kenarlara ait bir yüksekliğe eşittir.

Şekilde; |AB|=|AC|, [DF]⊥[AC], [DE]⊥[AB] ise; |BN|=|ED|+|DF| dir.

Özel Üçgen Formülleri

İkizkenar bir üçgende taban üzerinden alınan bir noktadan eşit kenarlara çizilen paralel doğru parçalarının uzunlukları toplamı, eş kenarların birinin uzunluğuna eşittir.

Özel Üçgen Formülleri

İkizkenar üçgenin tabanının uzantısı üzerinde alınan bir noktadan üçgenin eşit kenarlarına inilen dikmelerin uzunlukları farkının mutlak değeri eşit kenarlara ait bir yüksekliğe eşittir.

Şekilde; |AB|=|AC|, [EP]⊥[AC], [EF]⊥[AF] ve [BN]⊥[AC] ise; |EP|-|EF|=|BN| dir.

Özel Üçgen Formülleri

İkizkenar bir üçgende tepe noktasından tabana çizilen doğru parçasının uzunluğunun karesi, eş kenarların birinin uzunluğunun karesi ile ayırmış olduğu kenar uzunlukları çarpımı farkına eşittir.

Şekildeki ABC üçgeninde |AB|=|AC|=b, |AD|=x, |BD|=m ve |DC|=n olmak üzere; x²=b²-m.n dir.

Özel Üçgen Formülleri

Şekilde ABC eşkenar üçgen, [DE]⊥[AE], [DT]⊥[BC],  [DF]⊥[AF] ise |AB|kök3/2=|ED|+|DF|-|DT| dir.

İç Açıortay Teoremi Formülü

Bir üçgende açıortay uzunluğu karşı kenarı komşu kenarları oranında böler.

Şekildeki ABC üçgeninde [AN] açıortay ise; |AB|/|BN|=|AC|/|CN| dir.

Dış Açıortay Teoremi Formülü

Şekildeki ABC üçgeninde [AD]; m(CAE) nin açıortayı, |CD|=x, |BC|=a, |AC|=b ve |AB|=c olmak üzere; x/(x+a)=b/c dir.

Dış Açıortay Formülleri

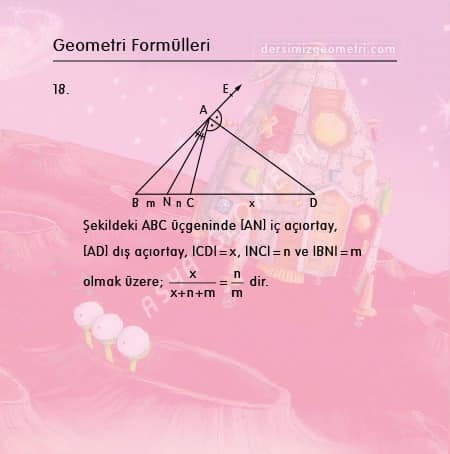
Şekideki ABC üçgeninde [AN] iç açıortay, [AD] dış açıortay, |CD|=x, |NC|=n ve |BN|=m olmak üzere; x/(x+n+m)=n/m dir.

Dış Açıortay Uzunluk Formülü

Şekildeki ABC üçgeninde [AD] dış açıortay, |CD|=x, |BC|=a, |AC|=b, |AB|=c ve |AD|=y olmak üzere; y²=x.(x+a)-bc dir.

Geometri Üçgende Alan Bağıntısı

Bir dik üçgende hipotenüse ait yükseklik, dik kenarlar uzunlukları çarpımının hipotenüs uzunluğuna bölümüdür.

Şekildeki ABC üçgeninde [BA]⊥[AC], [AD]⊥[BC], |AB|=c br, |AC|=b br, |BC|=a br ve |AD|=h br olmak üzere; h=(c.b)/a birimdir.

Üçgende Alan Kuralları

Herhangi bir ABC üçgeninde bir kenara ait kenarortay uzunluğu üçgenin alanını iki eşit alana ayırır.

Şekildeki ABC üçgeninde |BF|=|FC| ise; Alan(ABF)=Alan(AFC) dir.

İç Açıortay Kuralları

Bir üçgende iki iç açıortay varsa üçüncüsü de iç açıortaydır.Bir üçgende iç açıortaylar üçgenin içinde bir noktada kesişirler.Bu nokta üçgenin iç teğet çemberinin merkezidir.

Şekildeki ABC üçgeninde [BP], [CP] açıortay ise; [AP] açıortaydır.

Kenarortay Teoremi Formülü

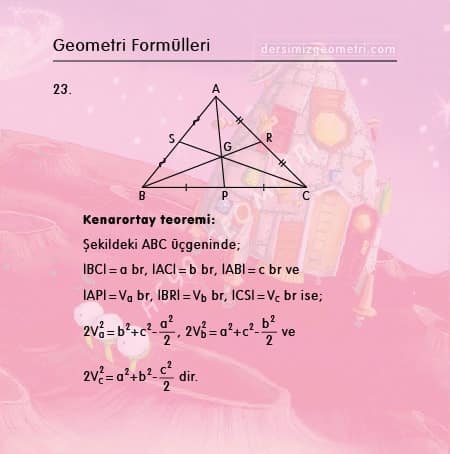
Şekildeki ABC üçgeninde BC|=a br, |AC|=b br, |AB|=c br, |AP|=Va br, |BR|=VB br, |CS|=VC br ise; 2Va²=b²+c²-a²/2, 2Vb²=a²+c²-b²/2 ve 2Vc²=a²+b²-c²/2 dir.

Kenarortay Ve U lu Alan Formülü

Bir ABC üçgeninin kenar uzunlukları a, b, c ve kenarortay uzunlukları Va, Vb, Vc olmak üzere; 4(Va²+Vb²+Vc²)=3(a²+b²+c²) dir.

Bir üçgenin iç teğet çemberinin yarıçapı r, kenar uzunlukları a, b, c ve u=(a+b+c)/2 ise; Alan(ABC)=u.r dir.

Üçgende Sinüslü Alan Formülü

Şekildeki ABC üçgeninde m(ADB)=α ise; içbükey-konkav dörtgenin alanı A(ABEC)=(1/2).|AE|.|BC|.sinα dır.

Dörtgende Sinüslü Alan Formülü

Herhangi bir dörtgende; köşegenler |CA|=e, |DB|=f ve arasındaki açı α olmak üzere; Alan(ABCD)=(1/2).e.f.sinα dır.

Dörtgen Formülleri

Köşegenleri dik kesişen dörtgende, karşılıklı kenarların kareleri toplamı birbirine eşittir.(a²+c²=b²+d²)

Dik Yamuk Formülü

Dik yamukta köşegenler birbirine dik ise yükseklik alt ve üst tabanın geometrik ortasıdır.(yüksekliğin karesi tabanların çarpımına eşittir.)

Şekildeki ABCD dörtgeninde [CD]⊥[DA], [DA]⊥[CD], [DB]⊥[AC], |AB|=a br, |CD|=c br ve |DA|=h br olmak üzere; h=√ac dir.

Yamukta Alan Kuralları

Bir yamukta yan kenarlardan birisinin orta noktası; karşı iki köşe ile birleştirildiğinde elde edilen üçgenin alanı, yamuğun alanının yarısına eşittir.

ABCD yamuk ve |CA|=|DB| ise; A(DAE)=(1/2).A(ABCD) dir.

Dörtgende Alan Kuralları

Bir dörtgenin kenarlarının orta noktaları birleştirilirse, bir paralelkenar oluşur.Bu paralelkenarın alanı, verilen dörtgenin alanının yarısına eşittir.Ayrıca paralelkenarın çevresi, dörtgenin köşegen uzunluklarının toplamına eşittir.

Şekildeki ABCD dörtgeninde N, P, K, L kenarlarının orta noktaları olmak üzere; A(NPKL)=(1/2).A(ABCD dir.

Paralelkenarda Alan Kuralları

Paralelkenar dışında alınan herhangi bir nokta, paralelkenarın köşelerine birleştirildiğinde elde edilen iki üçgenin alanları toplamı paralelkenarın alanının yarısına eşittir.

Şekilde ABCD paralelkenar ve dışında alınan bir P noktası olmak üzere; A(PDA)+A(PBC)=(1/2).A(ABCD dir.