Dik ve Özel Üçgenler Test-4

Matematik derslerinde 9. sınıf öğrencileri, özel üçgenlerin özelliklerini öğrenirken sık sık karşılaşırlar. Bu özel üçgenler, dik ve çeşitli özelliklere sahip üçgenler olarak bilinir. Bu test, öğrencilerin bu özel üçgenlerin özelliklerini anlamalarını ve uygulamalarını sağlayacak sorular içermektedir.

Problem 1 :

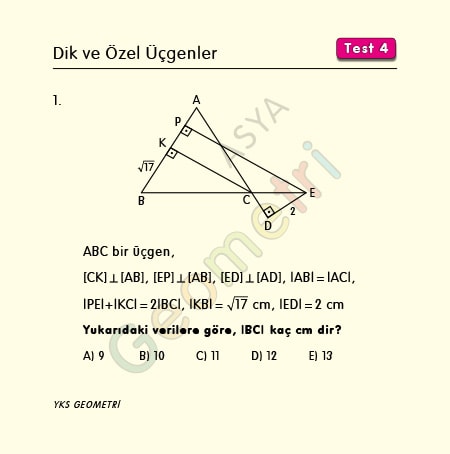
ABC bir üçgen, [CK] Ʇ [AB], [EP] Ʇ [AB], [ED] Ʇ [AD], |AB|=|AC|, |PE|+|KC|= 2|BC|, |KB|=√17 cm, |ED|=2 cm  ise; |BC| kaç cm dir?

Problem 2 :

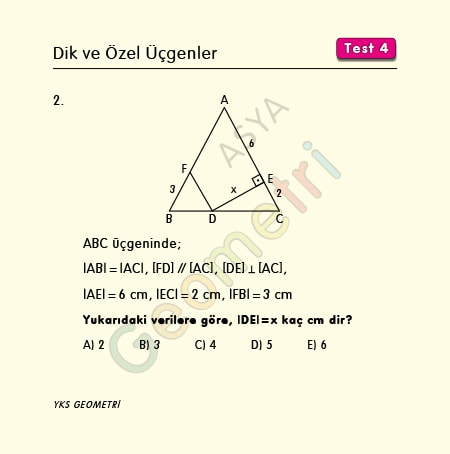
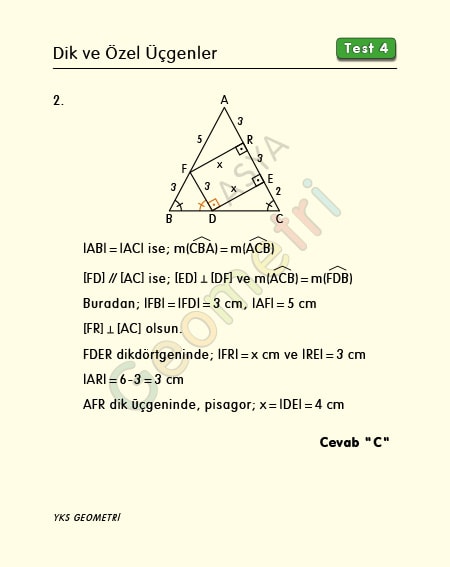
ABC üçgeninde |AB|=|AC|, [FD] // [AC], [DE] Ʇ [AC], |AE|=6 cm, |EC|= 2 cm, |FB|=3 cm ise; |DE|=x kaç cm dir?

Problem 3 :

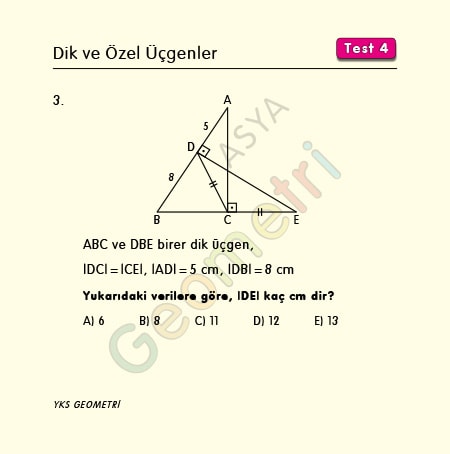
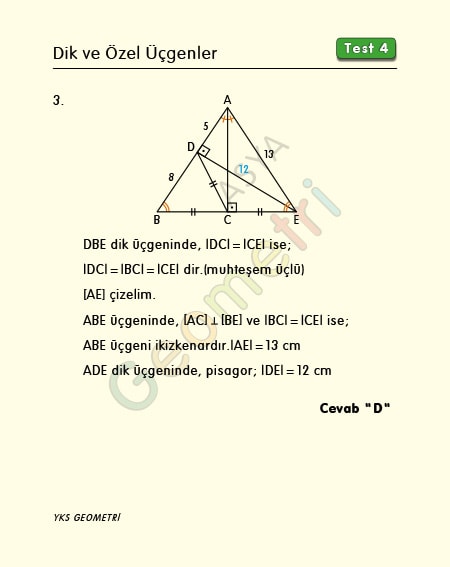
ABC ve DBE birer dik üçgen, |DC|=|CE|, |AD|=5 cm, |DB|= 8 cm ise; |DE| kaç cm dir?

Problem 4 :

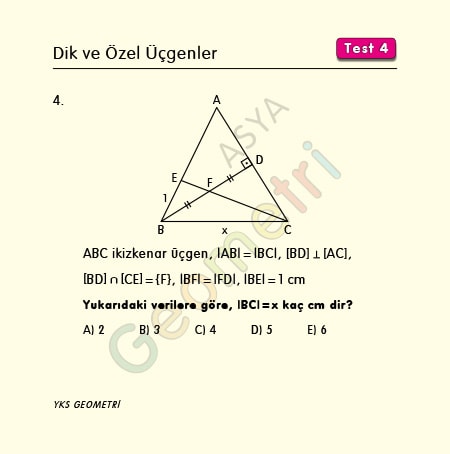
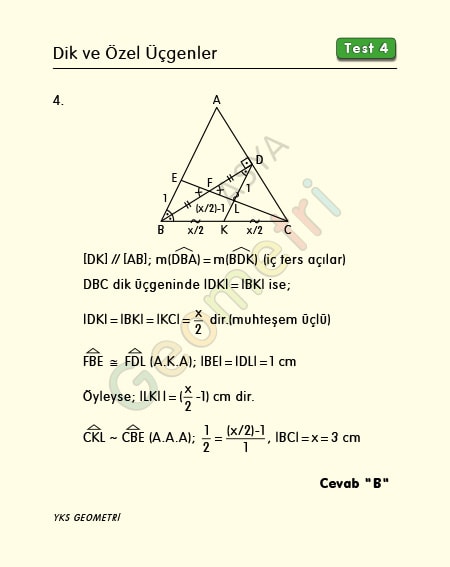
ABC ikizkenar üçgen, |AB|=|BC|, [BD] Ʇ [AC], [BD] ile [CE] nin kesim noktası F,  |BF|=|FD|, |BE|=1 cm, |BC|=x kaç cm dir?

Problem 5 :

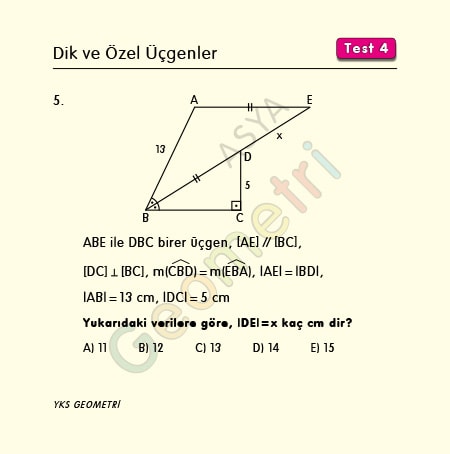
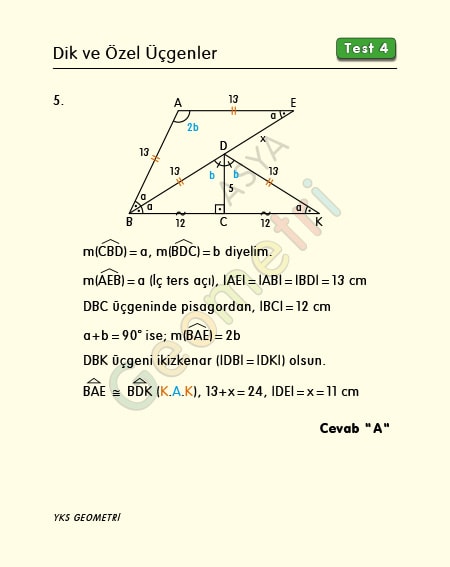
ABE ile DBC birer üçgen, [AE] // [BC], [DC] Ʇ [BC], m(CBD)=m(EBA), |AE|=|BD|, |AB|=13 cm, |DC|=5 cm ise; |DE|=x kaç cm dir?

Problem 6 :

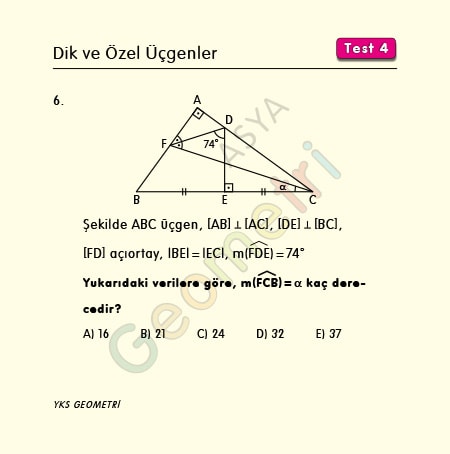
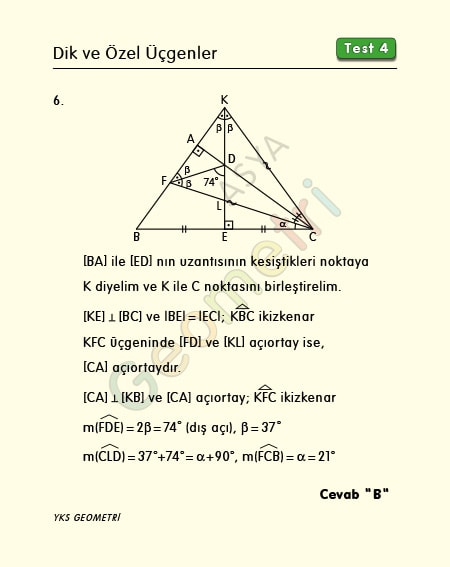
Şekilde ABC üçgen, [AB] Ʇ [AC], [DE] Ʇ [BC], [FD] açıortay, |BE|=|EC|, m(FDE)=74° ise; m(FCB)=α kaç derecedir?

Problem 7 :

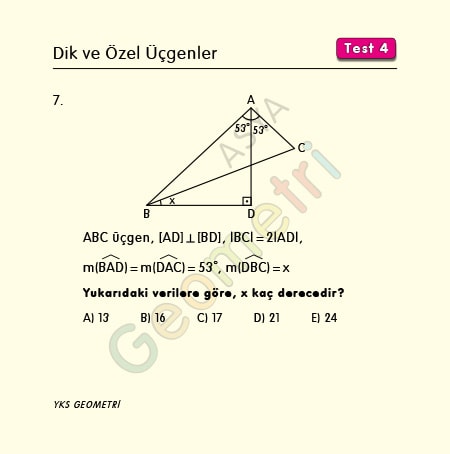
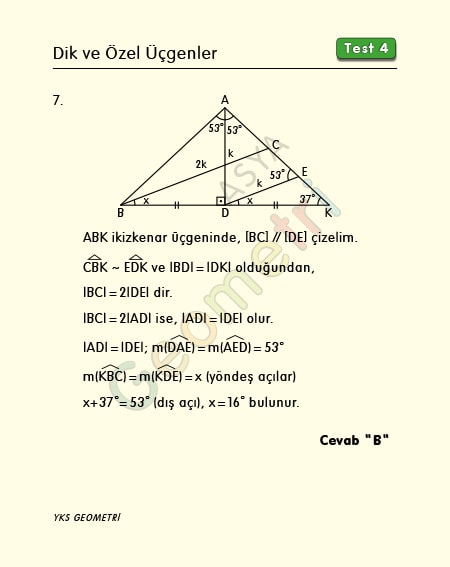
ABC üçgen, [AD] Ʇ [BD], |BC|=2|AD|, m(BAD)=m(DAC)=53° ise; m(DBC)= x kaç derecedir?

Problem 8 :

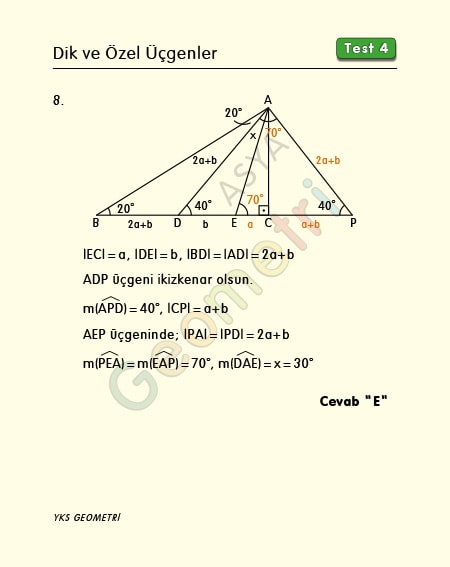
ABC dik üçgen, |BE|=2|CD|, m(CBA)=20°, m(CDA)=40° ise; m(DAE)= x kaç derecedir?

Dik ve Özel Üçgenler Test-4 Çözümleri

Problem 1’in çözümü :

|BC|= x dersek, |PE|+|KC|= 2x olur. ABC ikizkenar üçgeninde |PE|=|KC|+|ED| dir. (ispatı için bakınız) |KC|+2+|KC|= 2x, buradan |KC|= x-1 olur. KBC üçgeninde pisagor bağıntısı yazılırsa, |BC|=x=9 cm bulunur.

Problem 2’nin çözümü :

ABC ikizkenar üçgeninde [FD], [AC] ye paralel ise yöndeş açılardan |FD|= 3 cm ve [ED] diktir. FDER dikdörtgen olduğundan |FR|= x cm, |RE|= 3 cm, |AF|= 8-3=5 cm, |AR|= 6-3=3 cm, AFR dik üçgeninde pisagordan x=4 cm bulunur.

Problem 3’ün çözümü :

Çözüm : DBC dik üçgeninde |DC|=|CE| ise |DC|=|BC|=|CE| (muhteşem üçlü) dir. |BC|=|CE| ve [AC] ye [BE] ye dik olduğundan A ile E noktasını birleştirirsek ABE üçgeni ikizkenar olur. |AC|=13 cm. ADE üçgeni 5-12-13 dik üçgeni olacağından |DE|=12 cm bulunur.

Problem 4’ün çözümü :

DBC üçgeninde |DK|=|BK| ise |DK|=|BK|=|KC| (muhteşem üçlü) dir. Eş üçgenlerden |DL|=1 cm olduğundan |DK|=(x/2)-1 olur. İki üçgenin benzerliğinden x=3 cm bulunur.

Problem 5’in çözümü :

DBK ikizkenar üçgeni ile ABE üçgeninin iki kenarı ve arasındaki açıları eşit olduğundan bu üçgenler eştir. DBC 5-12-13 dik üçgeni olacağından |BC|=12 cm dir. |BK|=|BE|=24 cm olur. Buradan |DE|=x=24-13=11 cm hesaplanır.

Problem 6’nın çözümü :

Çözüm : [BA] ile [ED] nin uzantısının kesiştikleri K noktasını C noktasına birleştirelim. Yükseklik aynı zamanda kenarortay olduğundan KBC ikizkenar üçgenidir. Bir üçgende iki iç açıortay varsa üçüncüsü de açıortaydır. Buna göre KFC üçgeninde [CA] açıortaydır. [CA] açıortayı hem de yükseklik olduğundan KFC üçgeni ikizkenardır. Taban açılarına 2β dersek, dış açıdan β=37° dir. m(CLD)=37°+74°=α+90° olduğundan m(FCB)=α=21° bulunur.

Problem 7’nin çözümü :

 [AC] ile [BD] nin uzantısının kesiştikleri K noktası ABK üçgenini ikizkenar yapar. D noktasından [AK] ya paralel çizersek |BD|=|DK| olduğundan üçgenlerin benzerlik oranı 2 olur ki |BC|=2|DE| dir. |BC|=2|AD| idi. Buna göre |AD|=|DE| olacağından m(AED)=53° ve yöndeş açılardan m(KDE)=x dir. x+37°=53°, x=16° hesaplanır.

Problem 8’in çözümü :

Çözüm :  Dış açıdan m(BAD)=20° dir. m(CBA)=m(BAD)=20° olduğundan |BD|=|AD| dir. |EC|=a, |DE|=b dersek, |BD|=2a+b olur. |BD|=|AD|=2a+b. ADP üçgeni ikizkenar olacak biçimde bir P noktası alalım. m(APD)=40°, |CP|=a+b dir. |AP|=|EP|=2a+b olduğundan AEP üçgeninde m(PEA)=m(EAP)=70° dir. x+40°=70°, x=30° bulunur.

Dik ve Özel Üçgenler test-4 PDF

Ders Geometri, ücretsiz olarak indirilebilen PDF formatında Dik ve Özel Üçgenler Test-4 PDF dosyasını sunar. Matematik alanında önemli bir yere sahip olan geometri dersi, öğrencilerimizin becerilerini güçlendirmek adına oldukça önemlidir. Bundan dolayı Ders Geometri ekibi, öğrencilerin geometri konularındaki yeteneklerini artırmak için özel olarak hazırlanmış testler sunmaktadır. Bu değerli içerik, ücretsiz olarak temin edilebilen PDF formatındadır.

Üçgen Testleri öğrencilere problem çözme becerilerini geliştirme fırsatı sağlamakta olup, özellikle üniversite giriş sınavları TYT ve AYT’ye hazırlanan öğrenciler için büyük bir destektir. Bu kaynak, geometri alanındaki anlayışı pekiştirmek ve sınav hazırlıklarını daha etkili hale getirmek isteyen her öğrencinin başvurabileceği değerli bir rehberdir.