Dik ve Özel Üçgenler Test-1

Dik üçgenler, özel üçgenler, 30-60-90 üçgeni, 45-45-90 üçgeni, 15-75-90 üçgeni gibi temel geometrik kavramlar, matematik öğreniminde temel taşlardır. Bu kavramlar, geometrinin temel prensiplerini oluşturur. Öklid’in geometrisi, cisimlerin uzayda nasıl konumlandığını anlamamıza yardımcı olurken, Pisagor teoremi, üçgenlerin kenarları arasındaki matematiksel ilişkiyi ortaya koyar. Muhteşem üçlü ise, bu kavramları bir araya getirerek çeşitli problemlerin çözümünde bize yol gösterir. Ayrıca, kenarlarına ve açılarına göre özel üçgenler, geometrinin temel yapı taşlarından biridir.

Bu soruların çözümleri de yapıldığından, kendi çözümlerinizle karşılaştırarak konunuzu daha da pekiştirebilirsiniz. Bu testler, geometri alanında daha derinlemesine anlayış sağlama ve matematik becerilerinizi geliştirme fırsatı sunar.

Görselleri inceleyebilir, sayfa sonundan PDF formatındaki 8.-9.-11. Sınıf dik ve özel üçgenler test-1 dosyasını bilgisayarınıza indirebilirsiniz.

Problem 1 :

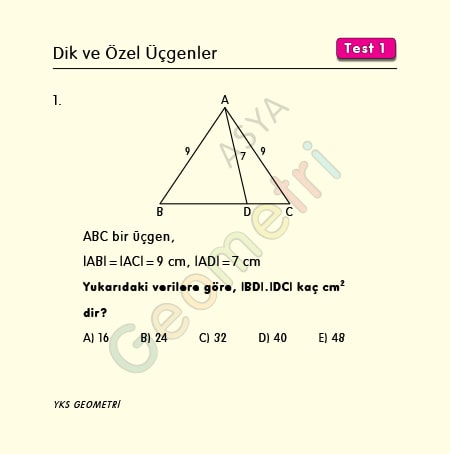
ABC bir üçgen, |AB|=|AC|=9 cm, |AD|=7 cm ise; |BD|.|DC| kaç cm² dir?

Problem 2 :

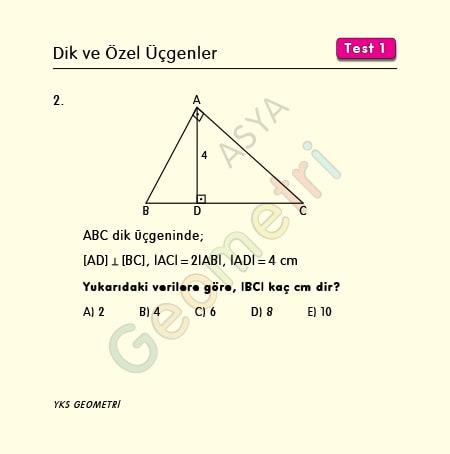
ABC dik üçgeninde, [AD] Ʇ [BC], |AC|=2|AB|, |AD|=4 cm ise; |BC| kaç cm dir?

Problem 3 :

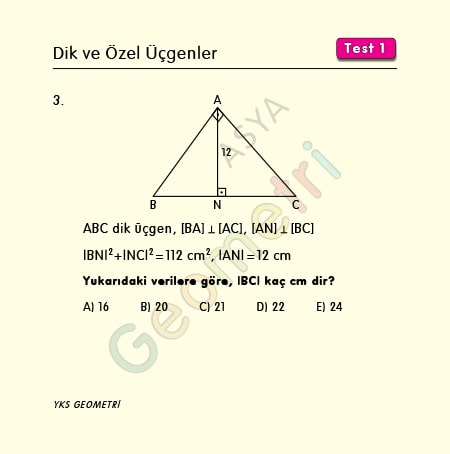
ABC dik üçgen, [BA] Ʇ [AC], [AN] Ʇ [BC],|BN|²+|NC|²=112 cm², |AN|=12 cm ise; |BC| kaç cm dir?

Problem 4 :

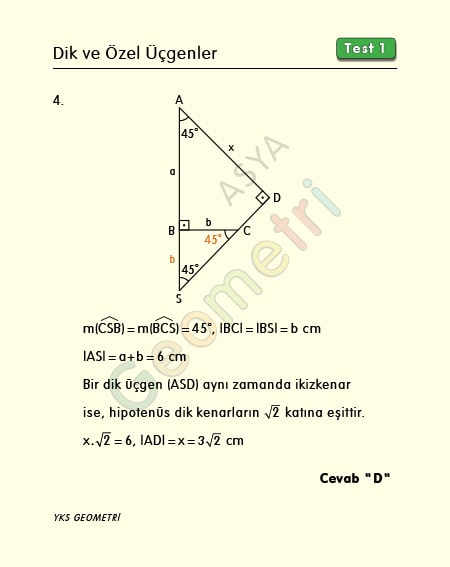
[AB] Ʇ [BC], [CD] Ʇ [AD], m(BAD)=45°, |AB|+|BC|=6 cm ise; |AD| kaç cm dir?

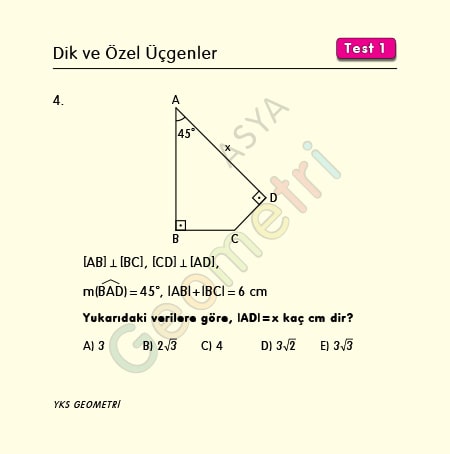
Problem 5 :

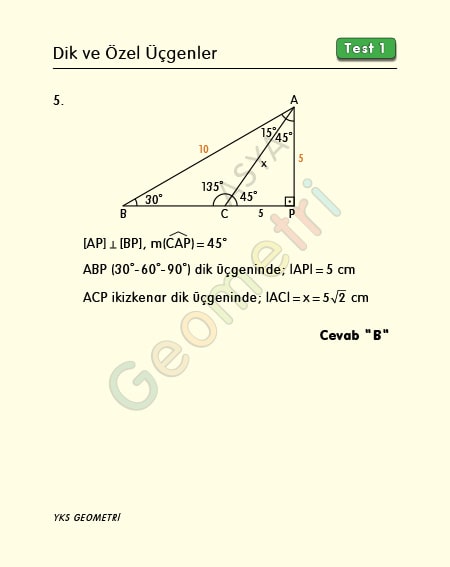
ABC bir üçgen, |AB|=10 cm, m(BAC)=15°, m(ACB)=135° ise; |AC|=x kaç cm dir?

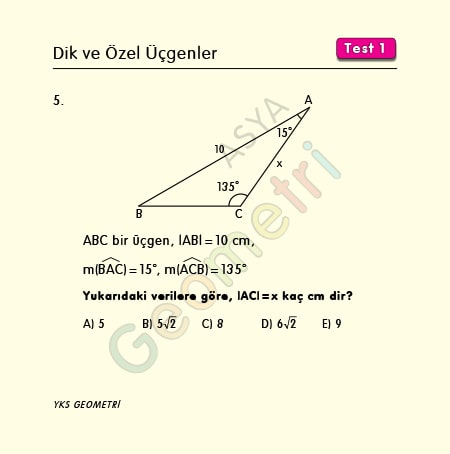
Problem 6 :

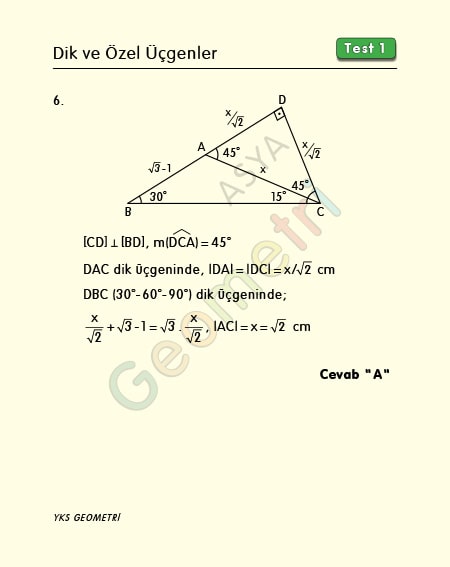
ABC bir üçgen, |AB|=(√3)-1 cm, m(ACB)=15°, m(CBA)=30° ise; |AC|=x kaç cm dir?

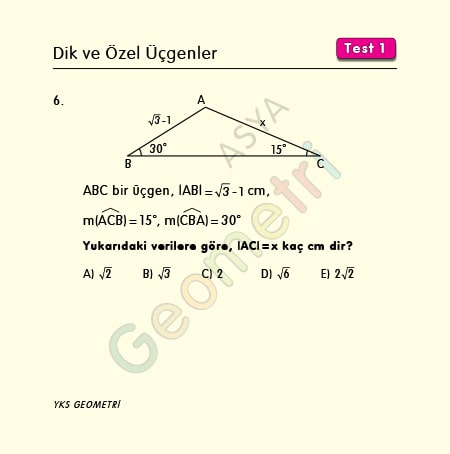
Problem 7 :

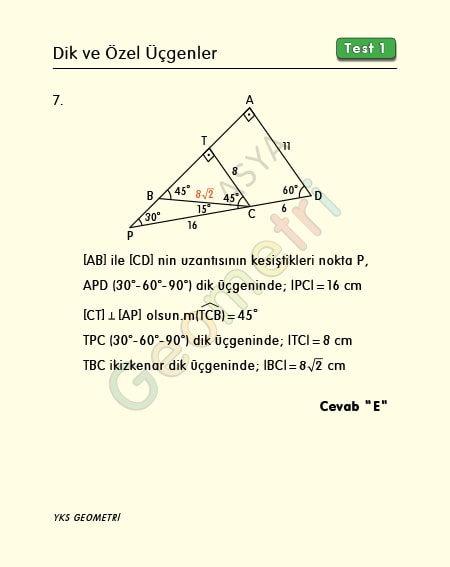
ABCD bir dörtgen, [BA] Ʇ [AD], m(ADC)=60°, m(CBA)=45°, |AD|=11 cm, |CD|=6 cm ise; |BC| kaç cm dir?

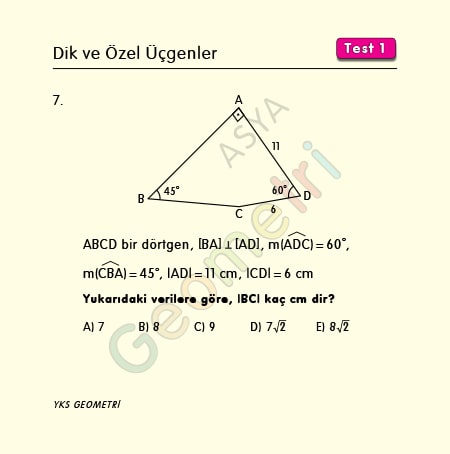
Problem 8 :

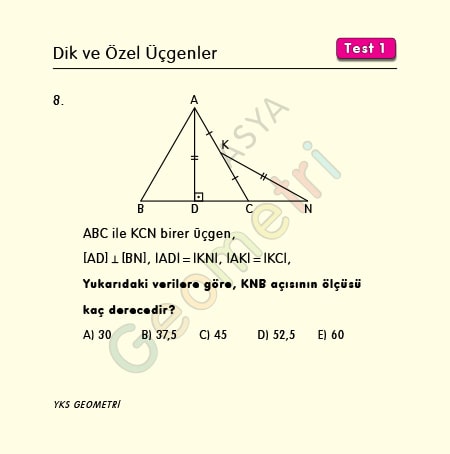
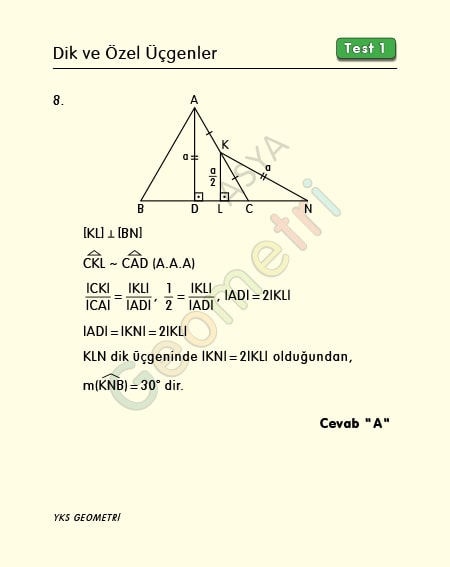
ABC ile KCN birer üçgen, [AD] Ʇ [BN], |AD|=|KN|, |AK|=|KC| ise; KNB açısının ölçüsü kaç derecedir?

Dik ve Özel Üçgenler Test-1 Çözümleri

Problem 1’in çözümü :

Bir ABC ikizkenar (|AC|=|BC|) üçgeninde, [BC] tabanının bir noktası D ise; |AD|²=|AB|²-|BD|.|DC| (x²=b-m.n) dir. 7²=9²-|BD|.|DC| yazılırsa, |BD|.|DC|=32 cm² bulunur.

Problem 2’nin 1. çözümü :

ABC üçgeninde pisagor bağıntısından |BC|=k.√5 dir. |BD|=x dersek; |DC|=k√5-x olur. ABC üçgeninde öklid bağıntısından k²=x.k√5, x=k/√5 olur. ABD üçgeninde pisagor bağıntısından k²=x²+16; x yerine k/√5 yazılırsa k=2√5 olacağından |BC|=10 cm bulunur.

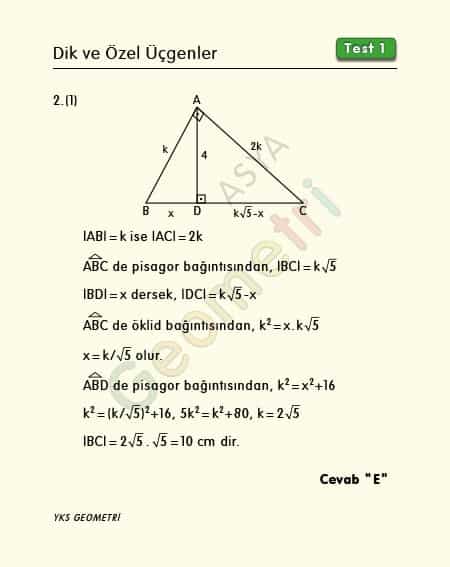
Problem 2’nin 2. çözümü :

Bir dik üçgende hipotenüse ait yükseklik dik kenarlar çarpımının hipotenüs’ e bölünmesi ile bulunur. Buna alan bağıntısı denir. Öklid teoremi konusu ile beraber işlenir. Bu formülün ispatı ve diğer formüllerin ispatı için geometri ispatlar bölümüne bakınız.

Problem 3’ün çözümü :

Bir dik üçgende hipotenüse ait yüksekliğin karesi köşelerden ayırdığı uzunlukların çarpımına eşittir. Buna öklid teoremi denir.

Problem 4’ün çözümü :

Dik üçgen aynı zamanda ikizkenar ise hipotenüs dik kenarların √2 katına eşittir.

Problem 5’in çözümü :

BC uzantısına A köşesinden dik inelim. Açılar yerine yazılır ve 30° nin karşısındaki kenar 5 deriz. İkizkenar dik üçgende hipotenüs dik kenarların √2 katına eşit olduğundan AC uzunluğuna 5√2 yazarız.

Problem 6’nın çözümü :

Bu soruların birçok çözüm yolu vardır. 30 60 90 üçgeni yada 45 45 90 üçgeni oluşturarak pratik bir şekilde çözüme gidebiliriz.

Problem 7’nin çözümü :

30 60 90 üçgeninde 30° nin karşısındaki kenar hipotenüs uzunluğunun yarısı kadardır ve bir ikizkenar dik üçgende hipotenüs dik kenarların √2 katına eşittir.

Problem 8’in çözümü :

Bir dik üçgende dik kenarlardan biri hipotenüs uzunluğunun yarısına eşit ise bu üçgen 30 60 90 üçgenidir ve yarısı olan kenarın karşısındaki köşe 30° dir.

Dik ve Özel Üçgenler test-1 PDF

Ders Geometri, ücretsiz olarak indirilebilen PDF formatında Dik ve Özel Üçgenler Test-1 PDF dosyasını sunar. Matematik alanında önemli bir yere sahip olan geometri dersi, öğrencilerimizin becerilerini güçlendirmek adına oldukça önemlidir. Bundan dolayı Ders Geometri ekibi, öğrencilerin geometri konularındaki yeteneklerini artırmak için özel olarak hazırlanmış testler sunmaktadır. Bu değerli içerik, ücretsiz olarak temin edilebilen PDF formatındadır.

Üçgen Testleri öğrencilere problem çözme becerilerini geliştirme fırsatı sağlamakta olup, özellikle üniversite giriş sınavları TYT ve AYT’ye hazırlanan öğrenciler için büyük bir destektir. Bu kaynak, geometri alanındaki anlayışı pekiştirmek ve sınav hazırlıklarını daha etkili hale getirmek isteyen her öğrencinin başvurabileceği değerli bir rehberdir.