Yamuk Test-1

TYT-AYT Geometri konuları yamuk test-1 ve çözümleri…
Problem 1 :
ABCD yamuk, [AB] paralel [DC], D açısının ölçüsü B açısının ölçüsünün iki katı, alt tabanın uzunluğu 13 cm, [AD] nin uzunluğu 8 cm ise; üst tabanın uzunluğu kaç cm dir?

Problem 2 :
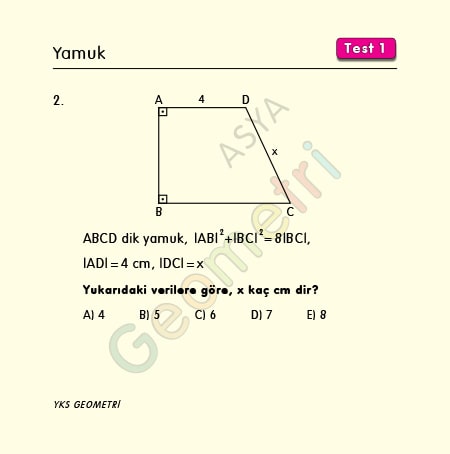
ABCD dik yamuk, |AB|²+|BC|²=8|BC|, üst tabanın uzunluğu 4 cm ise; yan kenar x kaç cm dir?
Problem 3 :
ABCD yamuk, [ED] dik [DC], E noktası alt tabanın orta noktası, 2|DA|=3|EB|, yükseklik 2kök5 cm ise; taralı alanların toplamı kaç cm² dir?

Problem 4 :
ABCD dik yamuğun köşegenleri birbirine dik , üst tabanın uzunluğu 3 cm, alt tabanın uzunluğu 8 cm ise; yan kenar x kaç cm dir?

Problem 5 :
ABCD ikizkenar yamuk, CAB dik üçgen, alt taban üst tabanın 3 katı, |AD|=6 cm, |CE|=|EB| ise; |AE|=x kaç cm dir?

Problem 6 :
ABCD dik yamuk, [DE] ve [CE] açıortay, |BC|=9 cm, |AB|=12 cm ise; ECD üçgenin alanı kaç cm² dir?

Problem 7 :
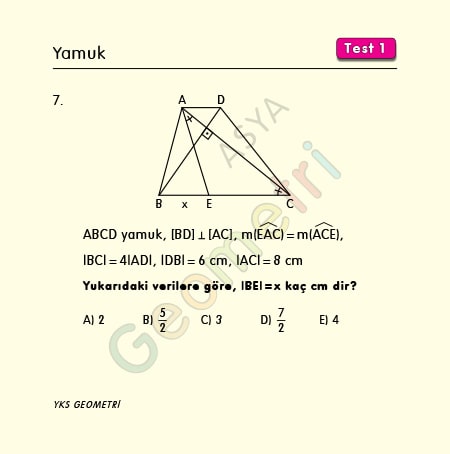
ABCD dik yamuk, köşegenleri 6 cm-8 cm ve birbirine dik, m(EAC)=m(AEC), alt taban üst tabanın 4 katı ise; |BE|=x kaç cm dir?
Problem 8 :
ABCD ikizkenar yamuk, |DB|=20 cm, m(CBD)=15° ise; yamuğun alanı kaç cm² dir?
Yamuk Test-1 Çözümleri
Problem 1’in çözümü :
Yamuk ABCD de [CE] [DA] ya paralel ve m(CBA)=α olsun. DAEC karşılıklı kenarları paralel dörtgen olduğundan paralelkenardır. Paralelkenarda karşılıklı açılar eşittir. m(ADC)=m(CEA)=2α dır. CEB üçgeninde m(CEA)=2α dış açı olduğundan m(ECB)=α dır. Buradan |EC|=|EB|=8 cm, |AE|=|DC|=13-8=5 cm bulunur.

Problem 2’nin çözümü :
Dik yamuk ABCD de [DH] [BC] ya dik ve |BC|=k dersek; ABHD dikdörtgen olacağından |AD|=|BH|=4 cm, |AB|=|DH|=n cm, |HC|=(k-4) cm dir. DHC üçgeninde pisagor bağıntısından n²+k²-8k+16=x² olur.n²+k² yerine 8k yazılırsa, 16=x², x=4 cm bulunur.

Problem 3’ün çözümü :
[DC] [AB] ye paralel olduğundan m(DEA)=90° olur. |AE|=|EB|=2x dersek |DA|=3x dir. DAE üçgeninde pisagor bağıntısından (3x)²=(2x)²+(2kök5)², 5x²=20, x=2 cm. DAE ile EBC üçgenlerinin taban uzunlukları ve yükseklikleri eşit olduğundan alanları eşittir. Alan(DAE)=4.2kök5/2=4kök5 cm², taralı bölgenin alanı=2A(DAE)=2.4kök5=8kök5 cm² bulunur.

Problem 4’ün çözümü :
Dik yamukta köşegenler birbirine dik ise yükseklik alt ve üst tabanın geometrik ortasıdır. h=karekök (a.c), h²=a.c, h²=3.8=24 cm² dir. Köşegenleri dik kesişen dörtgende, karşılıklı kenarların kareleri toplamı birbirine eşittir.h²+x²=3²+8², 24+x²=3²+8², |BC|=x=7 cm bulunur.

Problem 5’in çözümü :
ABCD ikizkenar yamukta yükseklik ([CP]) çizersek B köşesinden ayırmış olduğu uzunluğu (|PB|) (|AB|-|DC|)/2 dir.|DC|=k ise |AB|=3k, |PB|=(3k-k)/2=k olur. CAB üçgeninde öklid bağıntısından 36=3k², |AC|²=2k.3k=6k²=72 cm² dir.CAE üçgeninde pisagor bağıntısından x²=|AC|²+3², x²=72+9, x=9 cm bulunur.

Problem 6’nın çözümü :
Karşı durumların açıortayları bir dik oluştururlar. m(CED)=90°.Bir açının açıortayı üzerinde alınan herhangi bir noktadan açının kollarına inilen dikmeler birbirine eşittir. |AE|=|EB|=|EF|=6 cm. Aynı zamanda dikmelerin köşeden ayırdığı kenar uzunlukları da birbirine eşittir. |AD|=|DF|, |BC|=|CF|=9 cm.ECD üçgeninde öklid bağıntısından; 6²=9.|DF|, |DF|=4 cm olur. Alan(ECD)=6.13/2=39 cm² bulunur.

Problem 7’nin çözümü :
[CB] uzantısından |AD|=|PB| olacak şekilde bir P noktası alır, A noktasına birleştirirsek APBD paralelkenar olur. |DB|=|AP|=6 cm, m(PAC)=90° dir. APC üçgeni 6-8-10 dik üçgenidir. |PC|=10 cm. |EC|=|AE| olduğundan |PE|=|EC|=|AE|=5 cm (muhteşem üçlü) |AD|=|PB|=k, |BC|=4k olur.5k=10 cm, k=2 cm dir. x=5-2=3 cm bulunur.

Problem 8’in çözümü :
[DE], [BC] ye ve [EF], [DB] ye dik olsun. DBE üçgeninde |EF|=20/4=5 cm olur.(15-75-90 üçgeninde hipotenüse ait yükseklik, hipotenüs uzunluğunun dörtte biri kadardır.)ABG ile CDE eş üçgen olduğundan alanları da eşittir. O halde ABCD ikizkenar yamuğun alanı GBED dikdörtgenin alanına eşittir. Bu durumda Alan(ABCD)=20.5=100 cm² dir.


Yamuk Test-1 PDF
Ders Geometri, ücretsiz olarak indirilebilen pdf formatında Geometri soru bankası kitabını sunar. Öğrencilerin problem çözme becerilerini geliştirmeyi amaçlanmaktadır. Adaylar üniversite giriş sınavı tyt ayt için önemli olan yamuk test-1 pdf dosyasını görüntüleyebilir.