Üçgende Alan Test-1

TYT-AYT Geometri konuları üçgende alan test-1 ve çözümleri …
Görselleri inceleyebilir, sayfa sonundan PDF formatındaki 7.-8.-9. Sınıf üçgende alan test-1 dosyasını bilgisayarınıza indirebilirsiniz.
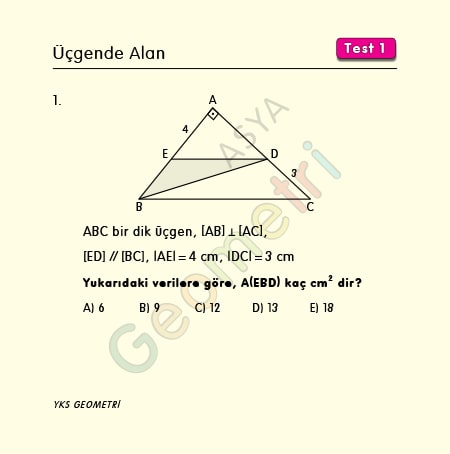
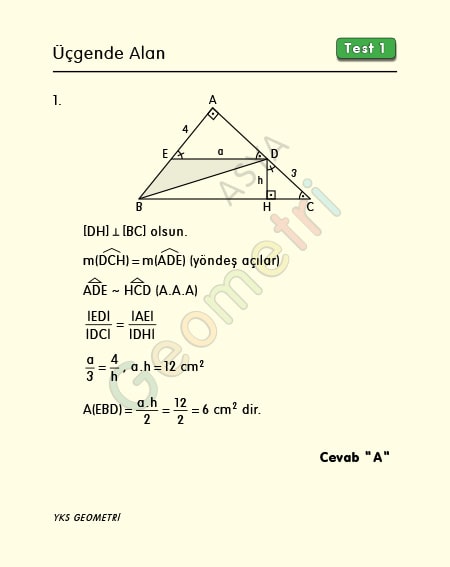
Problem 1 :
ABC bir dik üçgen, [AB] Ʇ [AC], [ED] paralel [BC], |AE|=4 cm, |DC|=3 cm ise; Alan (EBD) kaç cm² dir?
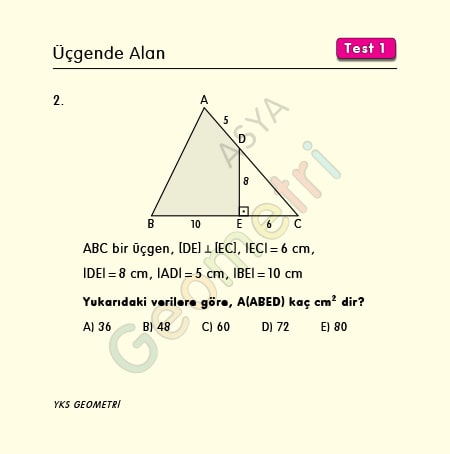
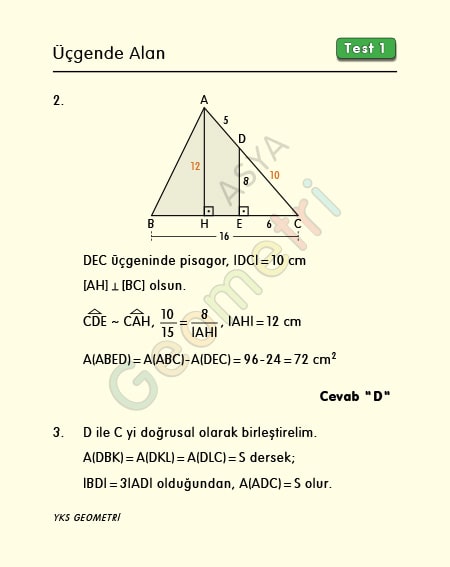
Problem 2 :
ABC bir üçgen, [DE] Ʇ [EC], |EC|=6 cm, |DE|=8 cm, |AD|=5 cm, |BE|=10 cm ise; Alan (ABED) kaç cm² dir?
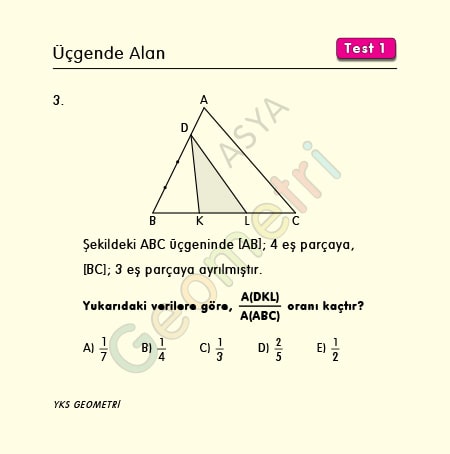
Problem 3 :
Şekildeki ABC üçgeninde [AB] 4 eş parçaya, [BC] 3 eş parçaya ayrılmıştır. Buna göre, Alan (DKL) / Alan (ABC) oranı kaçtır?
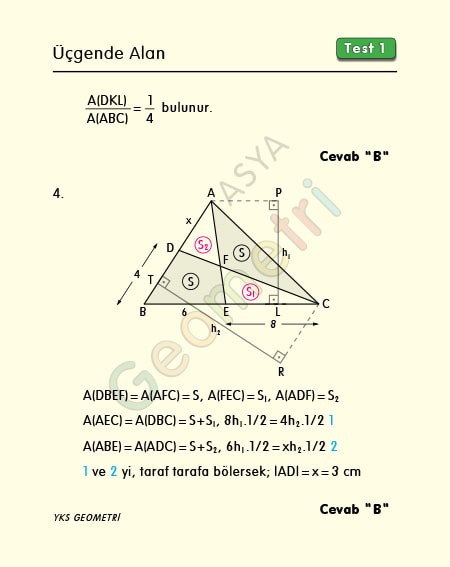
Problem 4 :
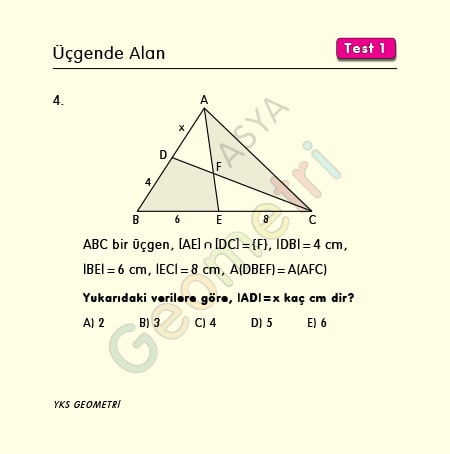
ABC bir üçgen, F noktası [AE] ile [DC] nin kesim noktası, |DB|=4 cm, |BE|=6 cm, |EC|=8 cm, Alan (DBEF) = Alan (AFC) ise; |AD|=x kaç cm dir?
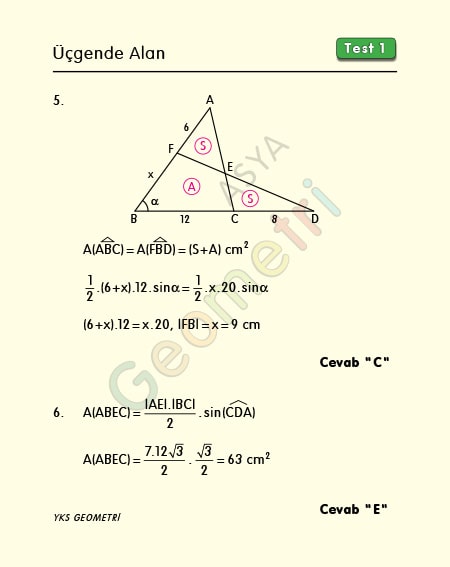
Problem 5 :
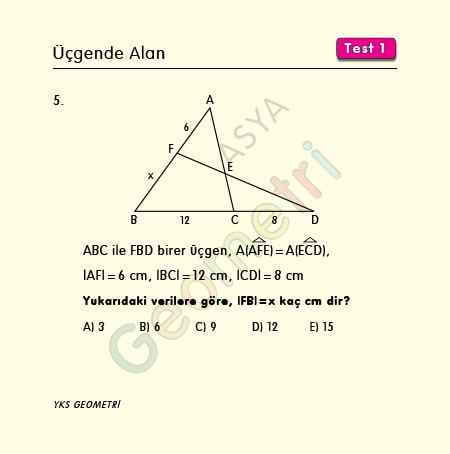
ABC ile FBD birer üçgen, Alan (AFE) = Alan (ECD), |AF|=6 cm, |BC|=12 cm, |CD|=8 cm ise; |FB|=x kaç cm dir?
Problem 6 :
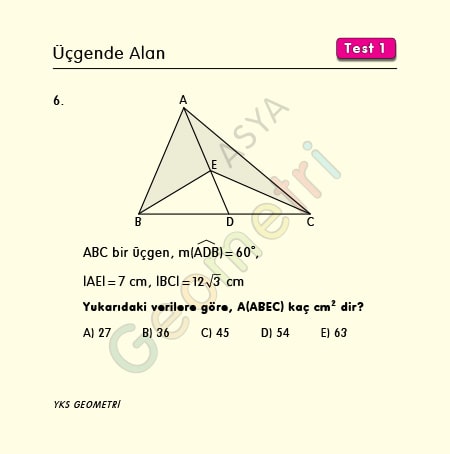
ABC bir üçgen, m(ADB)=60°, |AE|=7 cm, |BC|=12√3 cm ise; Alan (ABEC) kaç cm² dir?
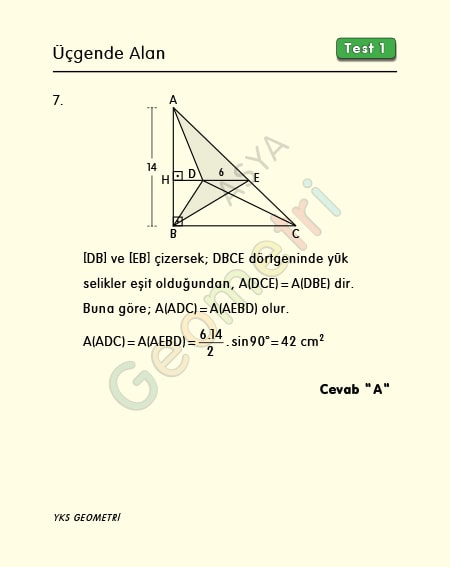
Problem 7 :
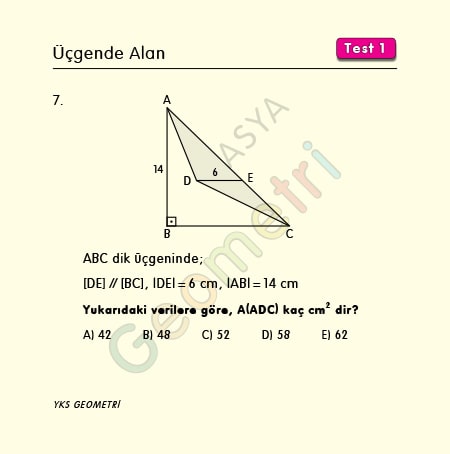
ABC dik üçgeninde, [DE] // [BC], |DE|=6 cm, |AB|=14 cm ise; Alan (ADC) kaç cm² dir?
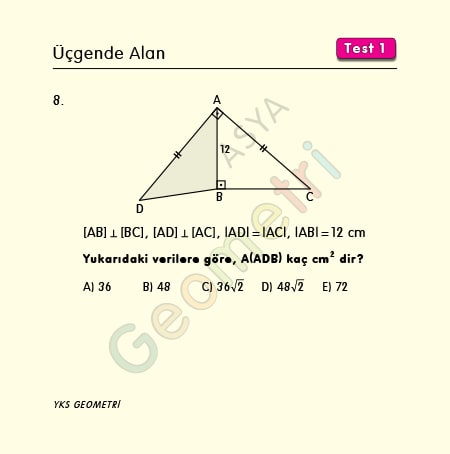
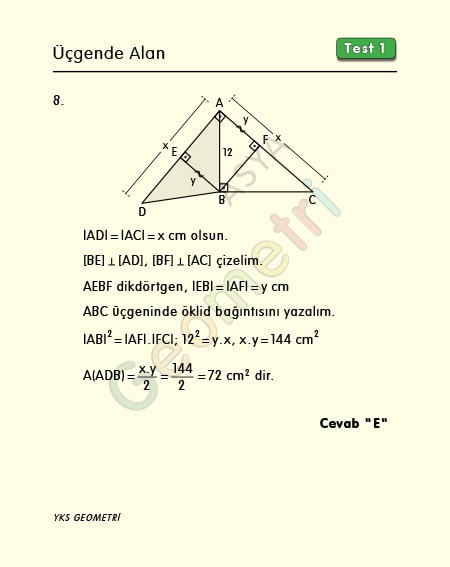
Problem 8 :
Şekilde [AB] Ʇ [BC], [AD] Ʇ [AC], |AD|=|AC|, |AB|=12 cm ise; Alan (ADB) kaç cm² dir?
Üçgende Alan Test-1 Çözümleri
Problem 1’in çözümü :
D noktasından BC kenarında dik çizersek ADE ve HCD üçgeninin tüm açıları eş olur. İki üçgeninin benzerlik oranından EDB üçgenine ait taban x yükseklik değeri ile EDB üçgenin alanı hesaplanır.
Problem 2’nin çözümü :
DEC dik üçgeni 6 8 10 üçgenidir. |DC|=10 cm. ABC üçgeninde A köşesinden tabana dik inersek, [DC] ye paralel olacağından benzer üçgenler oluşur. Benzerlik oranından |AH|=12 cm. İki üçgenin alanı bilindiğinden, taralı bölgenin alanı=96-24=72 cm² bulunur.
Problem 3’ün çözümü :
D ile C noktasını birleştirirsek. oluşan DBC deki üçgeninin tabanı eşit parçalara bölündüğünden, üç üçgenin alanları eşittir. Alan (DBC) = 3S.|BD| = 3|AD| olduğundan Alan (ADC)=S olur. Alan (DKL) / Alan (ABC) = 1/4 tür.
Problem 4’ün çözümü :
[BC] ve [AB] kenarına ait yüksekliklere h1 ve h2 ile isimlendirip eşit alanlar (S+S1), (S+S2) den 2 eşitlik yazıp taraf tarafa bölersek x değeri bulunur.
Problem 5’in çözümü :
Çözüm 5 : Eşit alanları harflendirirsek, ABC üçgeninin alanı ile FBD üçgenin alanı eşit olur. Alanları iki kenarı ve aralarındaki açının cinsinden yazar, birbirine eşitlersek istenen x uzunluğu buluruz.
Problem 6’nın çözümü :
Şekildeki ABEC içbükey dörtgenin alanı büyük üçgenin (ABC) alanından küçük üçgenin (EBC) alanını çıkarılması ile bulunur. Çözümü kolaylaştırmak için formülleştirdik. Bu formülün ispatına geometri formülleri sayfa sonundan Geometri Formüllerinin İspatları PDF dosyasıyla erişebilirsiniz
Problem 7’nin çözümü :
ABC dik üçgeninde [DB] ve [EB] çizersek; oluşan DBCE dörtgeninde [DE], [BC] ye paralel ( yamuk ) olduğundan DEC üçgenin alanı DEB üçgenin alanına eşittir. Taralı bölgenin alanı AEBD içbükey dörtgeninin alanına eşit olur. Alan (AEBD)=(6.14)/2=42 cm² bulunur.
Problem 8’in çözümü :
Verilen içbükey dörtgenin şeklini dikkate alalım. B noktasından AC’ye ve AD’ye dik çizimler yapalım. Bu durumda, AEBF dikdörtgeninde EB’nin uzunluğu AF’nin uzunluğuna eşittir. |EB|=|AF|=y diyelim.
|AD|=|AC| verilmiş buna da x diyelim.
Şimdi, ABC üçgeninde öklid bağıntısını yazalım. 12² = y.x , 144 = y.x
Alan (ADB)= x. y. (1/2) olduğunu biliyoruz. Yani, ADB üçgeninin alanı x.y’nin yarısını oluşturur. O halde cevap 72 cm² olacaktır.
Üçgende Alan test-1 PDF

Ders Geometri, ücretsiz olarak indirilebilen PDF formatında Üçgende Alan Test-1 PDF dosyasını sunar. Matematik alanında önemli bir yere sahip olan geometri dersi, öğrencilerimizin becerilerini güçlendirmek adına oldukça önemlidir. Bundan dolayı Ders Geometri ekibi, öğrencilerin geometri konularındaki yeteneklerini artırmak için özel olarak hazırlanmış testler sunmaktadır. Bu değerli içerik, ücretsiz olarak temin edilebilen PDF formatındadır.
Üçgen Testleri öğrencilere problem çözme becerilerini geliştirme fırsatı sağlamakta olup, özellikle üniversite giriş sınavları TYT ve AYT’ye hazırlanan öğrenciler için büyük bir destektir. Bu kaynak, geometri alanındaki anlayışı pekiştirmek ve sınav hazırlıklarını daha etkili hale getirmek isteyen her öğrencinin başvurabileceği değerli bir rehberdir.