Üçgende Açıortay Test-1

TYT-AYT Geometri konuları üçgende açıortay test-1 ve çözümleri…
Problem 1 :
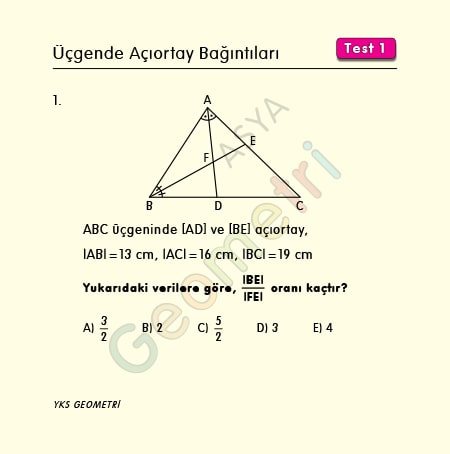
ABC üçgeninde [AD] ve [BE] açıortay, |AB|=13 cm, |AC|=16 cm, |BC|=19 cm ise; |BE|/|FE| oranı kaçtır?
Problem 2 :
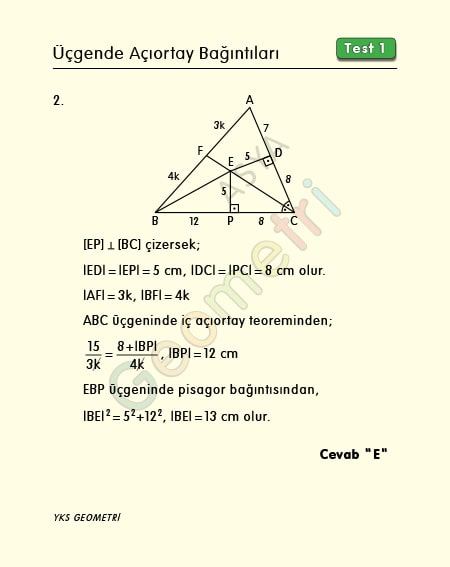
ABC üçgeninde [ED] Ʇ [AC], [CF] açıortay, 3|BF|=4|AF|, |ED|=5 cm, |AD|=7 cm, |DC|=8 cm ise; |BE| kaç cm dir?

Problem 3 :
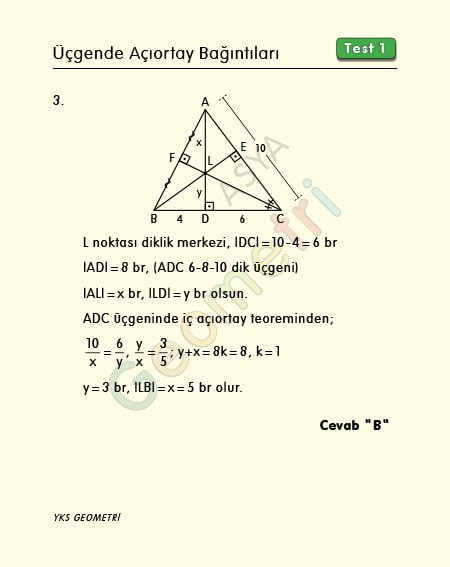
ABC bir üçgen, [AD] Ʇ [BC], |AC|=|BC|, |BD|=4 br ise; ABC üçgenin diklik merkezinin B köşesine uzaklığı kaç br dir?

Problem 4 :
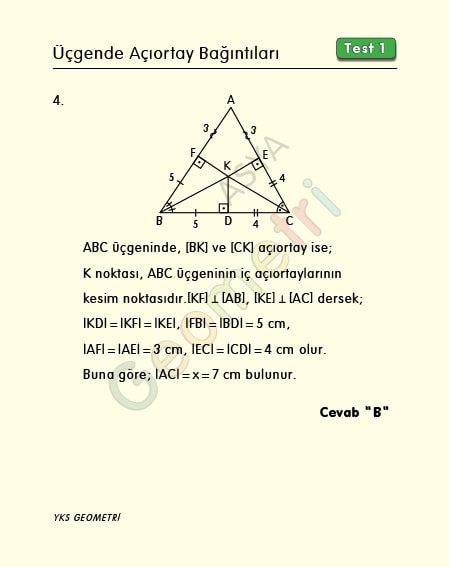
ABC üçgeninde [BK] ve [CK] açıortay, [KD] Ʇ [BC], |AB|=8 cm, |BD|=7 cm, |DC|=4 cm ise; |AC|=x kaç cm dir?

Problem 5 :
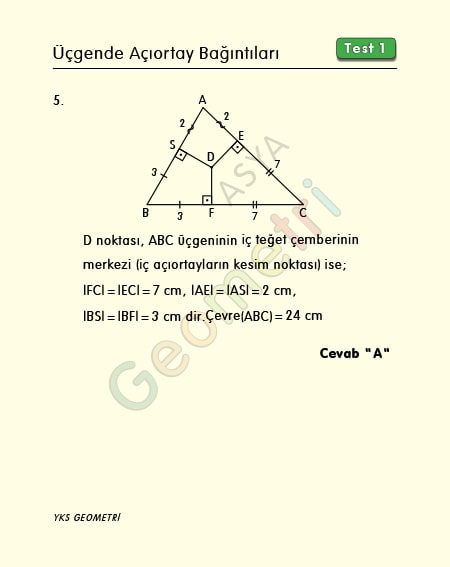
D noktası ABC üçgeninin iç teğet çemberinin merkezi, [DE] Ʇ [AC], [DF] Ʇ [BC], |AB|=5 cm, |FC|=7 cm, |AE|=2 cm ise; Çevre(ABC) kaç cm dir?

Problem 6 :
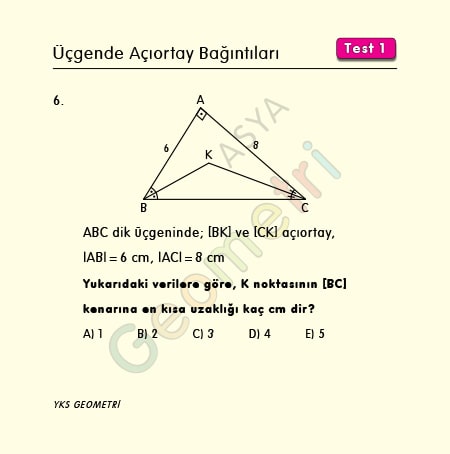
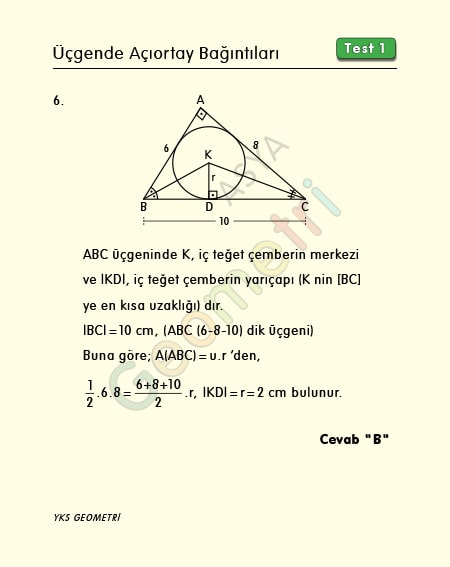
ABC dik üçgeninde [BK] ve [CK] açıortay, |AB|=6 cm, |AC|=8 cm ise; K noktasının [BC] kenarına en kısa uzaklığı kaç cm dir?
Problem 7 :
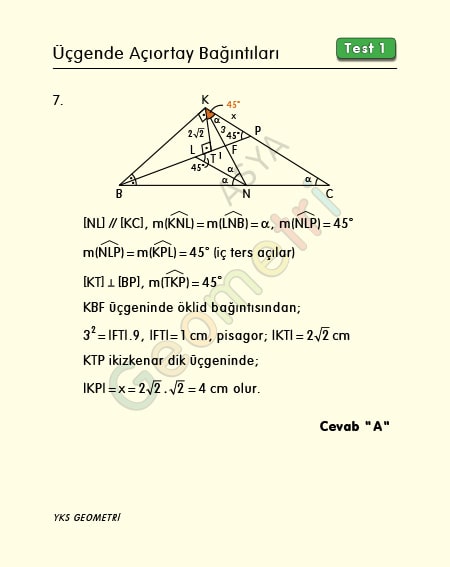
KBC üçgeninde [BK] Ʇ [KN], m(CBP)=m(PBK), |KN|=|NC|, |KF|=3 cm, |BF|=9 cm ise; |KP|=x kaç cm dir?

Problem 8 :
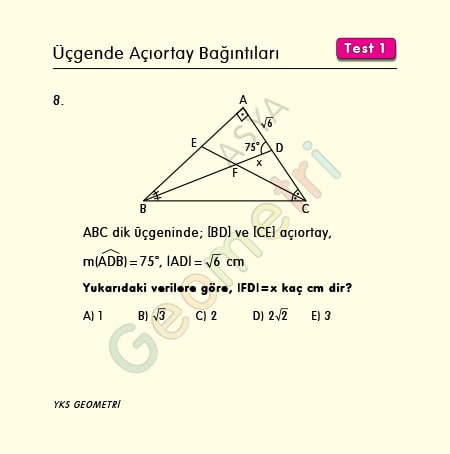
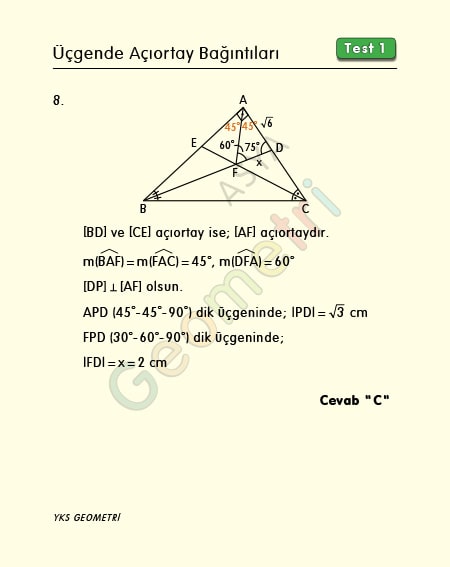
ABC dik üçgeninde [BD] ve [CE] açıortay, m(ADB)=75°, |AD|=√6 cm ise; |FD|=x kaç cm dir?
Üçgende Açıortay Test-1 Çözümleri
Problem 1’in çözümü :
Üçgende açıortayların kesim noktası sorusu, iç açıortay teoremi yardımıyla çıkarılan formülden çözülmüştür.

Problem 2’nin çözümü :
Bir açının açıortayı üzerinde alınan herhangi bir noktadan, açının kollarına inilen dikmeler ile dikmelerin köşeden ayırdığı kenar uzunlukları birbirine eşit olduğundan |ED|=|EP|=5 cm, |DC|=|PC|=8 cm olur. ABC üçgeninde iç açıortay teoreminden |BP|=12 cm, EBP (5 12 13) üçgeninde hipotenüs 13 cm dir.
Problem 3’ün çözümü :
ABC üçgenine ait diğer yükseklikler de çizilirse, yüksekliklerin kesim noktası diklik merkezi olur. ADC dik üçgeninde dik kenar 6 br ve hipotenüs 10 br ise, üçüncü kenar 8 br dir. (6 8 10 dik üçgeni). ABC ikizkenar üçgeninde [CF] yükseklik aynı zamanda açıortay olur. ADC üçgeninde iç açıortay teoreminden x=5 br, y=3 br hesaplanır. Diklik merkezinin B köşesine uzaklığı=x=5 br bulunur.
Problem 4’ün çözümü :
Bir açının açıortayı üzerinde alınan herhangi bir noktadan, açının kollarına inilen dikmeler ile dikmelerin köşeden ayırdığı kenar uzunlukları birbirine eşittir. Buna göre x değeri bulunur.
Problem 5’in çözümü :
ABC üçgeninin iç teğet çemberin merkezinden köşelere birleştiren doğru parçaları açıortaydır ve dikmelerin köşeden ayırdığı kenar uzunlukları eşittir. Buna göre |FC|=|EC|=7 cm, |AE|=|AS|=2 cm, |BS|=|BF|=3 cm olur. ABC üçgeninin çevresi 24 cm bulunur.
Problem 6’nın çözümü :
Açıortay testindeki bu soru da ise K noktasının [BC] kenarına en kısa uzaklığını bulmamızı istiyor. En kısa uzaklık o kenara ait yüksekliktir. ABC üçgeninde K noktasından [BC] ye dik inersek, |KD| iç teğet çemberin yarıçapıdır çünkü K noktası üçgende iki iç açıortayın kesim noktasıdır. ABC üçgeninde hipotenüs 10 cm olur (6 8 10 üçgeni). Bir üçgenin alanı yarı çevre ile yarıçapın çarpımıdır. A(ABC)=u.r, 24=12.r, |KD|=r=2 cm bulunur.
Problem 7’nin çözümü :
[NL], [KC] ye paralel olsun. m(KNL)=m(LNB)=α, NLP açısı ise üçgende iki iç açıortay olduğundan 45° dir. İç ters açılardan m(NLP)=m(KPL)=45° olur. K noktasından [BP] ye dik inersek, m(TKP)=45° dir. KBF üçgeninde öklid bağıntısından |FT|=1 cm dir. Pisagordan KT uzunluğu 2√2 cm olur. 45 45 90 üçgeninde 45° nin karşısındaki kenar 2√2 cm olduğundan hipotenüs (x) 4 cm olur.
Problem 8’in çözümü :
Bir üçgende iki iç açıortay var ise, üçüncüsü de açıortaydır. Açıortayların kesim noktası olduğu için iç teğet çemberin merkezi olur. Tersi içinde geçerlidir. İspatını geometri soru bankası pdf de basitleştirerek yaptık. Çözüme gelirsek, A ile F noktasını birleştirelim. A köşesindeki açılar 45 er derece olur. AFD üçgeninde üçüncü açısı 60 dir. D noktasından [AF] ye dik çizersek, 45 45 90 ve 30 60 90 üçgeni ile istenen x uzunluğu 2 cm hesaplanır.

Üçgende Açıortay Test-1 PDF
Ders Geometri, ücretsiz olarak indirilebilen pdf formatında Geometri soru bankası kitabını sunar. Öğrencilerin problem çözme becerilerini geliştirmeyi amaçlanmaktadır. Adaylar üniversite giriş sınavı tyt ayt için önemli olan üçgende açıortay test-1 pdf dosyasını görüntüleyebilir.