Dik ve Özel Üçgenler Test-2

TYT AYT Geometri konuları dik ve özel üçgenler test-2 ve çözümleri…

30 60 90 üçgeni soruları, 45 45 90 üçgeni ile ilgili sorular, 15 75 90 üçgeni soruları, diklik merkezi soruları, muhteşem üçlü soruları, özel üçgen soru, pisagor bağıntısı soruları, 30 60 90 üçgeni çözümlü sorular, diklik merkezi soru çözümü, 15 75 90 üçgeni soru çözümü, pisagor çözümlü sorular

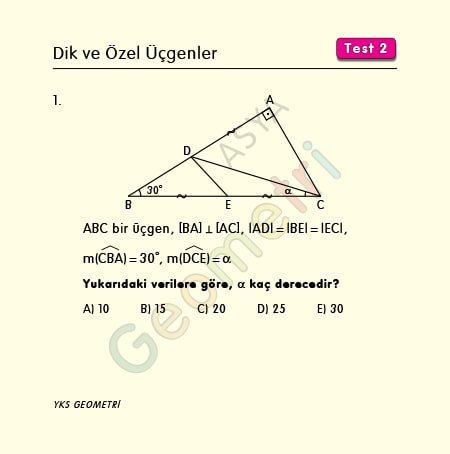
Problem 1 :

ABC bir üçgen, [BA] Ʇ [AC], |AD|=|BE|=|EC|, m(CBA)=30° ise; m(DCE)=α kaç derecedir?

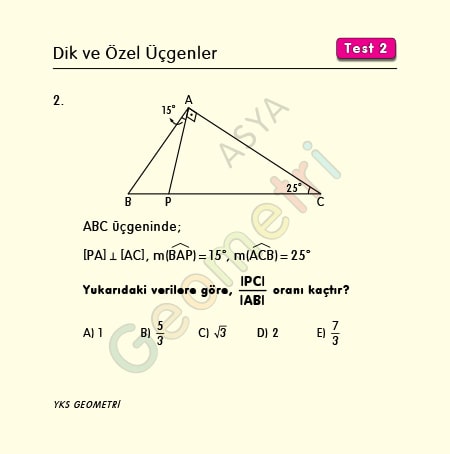
Problem 2 :

ABC bir üçgen, [PA] Ʇ [AC], m(BAP)=15°, m(ACP)=25° ise; |PC|/|AB| oranı kaçtır?

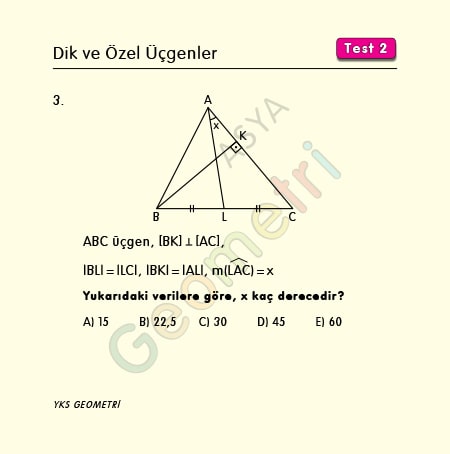
Problem 3 :

ABC bir üçgen, [BK] Ʇ [AC], |BL|=|LC|, |BK|=|AL| ise; m(LAC)=x kaç derecedir?

Problem 4 :

[BD] üzerindeki E noktası ABC üçgeninin yüksekliklerinin kesim noktası, |BE|=4√3 cm, |ED|=√3 cm, m(ACB)=60° ise; |AC|=x kaç cm dir?

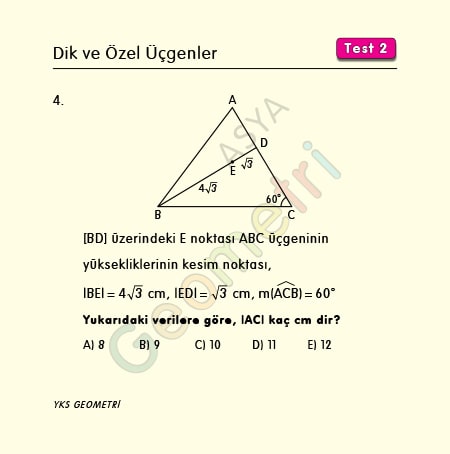
Problem 5 :

ABC dik üçgen, [BA] Ʇ [AC], [AE] Ʇ [BC], |BD|=|DC|, |AD|=10 cm, m(ACB)=15° ise; |AE|=x kaç cm dir?

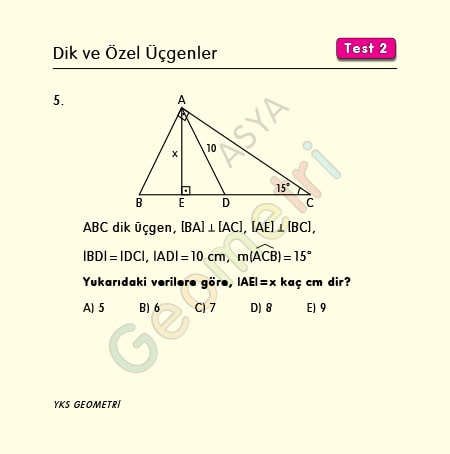
Problem 6 :

ABC bir üçgen, [DA] Ʇ [AC], m(BAD)=45°, |AD|=√2 cm, |AC|=2√2 cm ise; |AB|=x kaç cm dir?

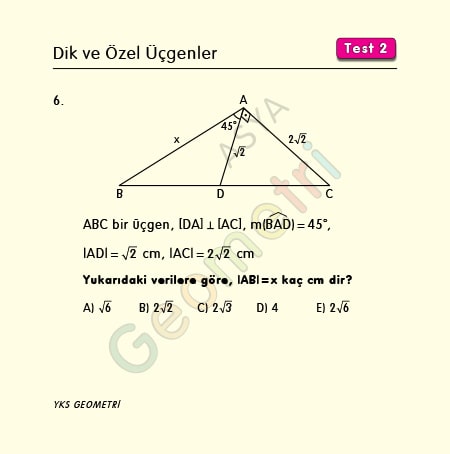
Problem 7 :

ABC üçgeninde A,D ve E noktası doğrusal, [AE] Ʇ [BC], |AD|=7 cm, |AC|=8 cm, |BD|=3 cm ise; |DC|=x kaç cm dir?

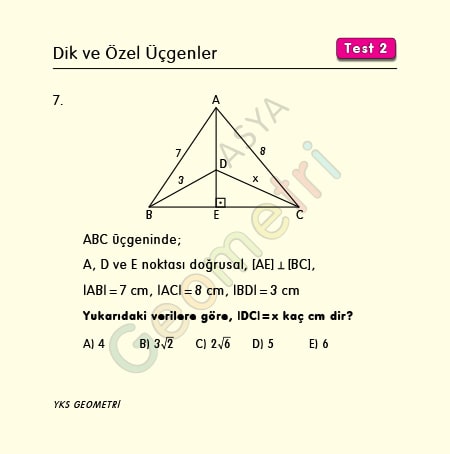
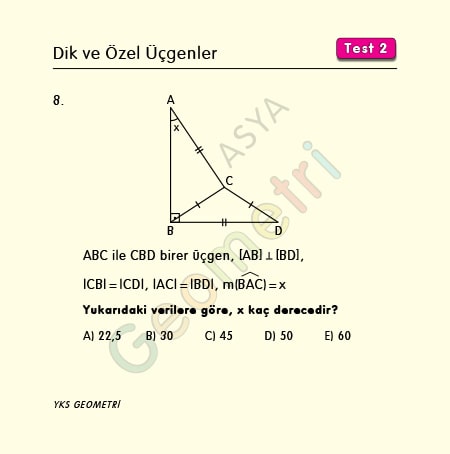
Problem 8 :

ABC ile CBD birer üçgen, [AB] Ʇ [BD], |CB|=|CD|, |AC|=|BD| ise; m(BAC)=x kaç derecedir?

Dik ve Özel Üçgenler Test-2 Çözümleri

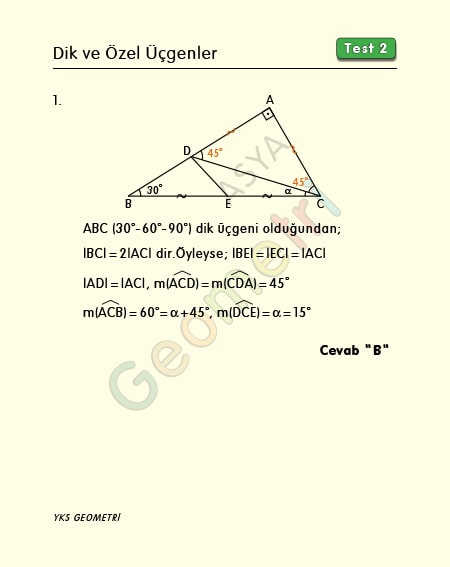
Problem 1’in çözümü :

ABC üçgeninde (30 60 90) hipotenüs uzunluğuna 2 br dersek 30° nin karşısındaki kenar 1 br dir. ABC üçgeni ikizkenar (45 45 90) olur ki α+45°=60° olacağından α=15° bulunur.

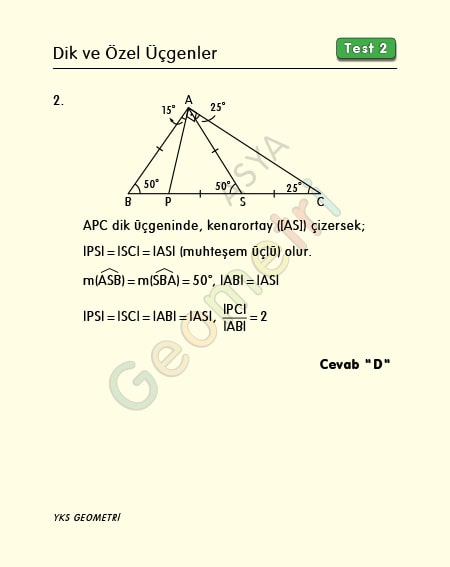
Problem 2’nin çözümü :

ABC üçgenin iç açıları toplamından B açısının ölçüsü 50° dir. APC dik üçgeninde hipotenüse ait kenarortay çizersek kenarortay uzunluğu hipotenüsün yarısına eşit olur (muhteşem üçlü-süper üçlü). Buna göre ABS üçgeninde m(ASB)=50° olur. Buradan |AB|=|AS| dir. O halde |PC|/|AB| oranı 2 dir.

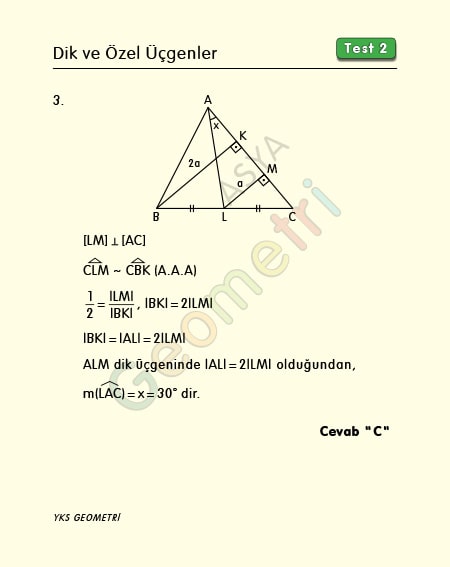
Problem 3’ün çözümü :

ABC üçgeninde taban iki eş parçaya bölündüğünden çizeceğimiz paralel benzer üçgenlerin oranı 2 yapar ki oluşan ALM dik üçgeninde hipotenüs dik kenarın 2 katı olur. Bu dik kenarın karşısındaki köşe x açısı, 30° olacaktır.

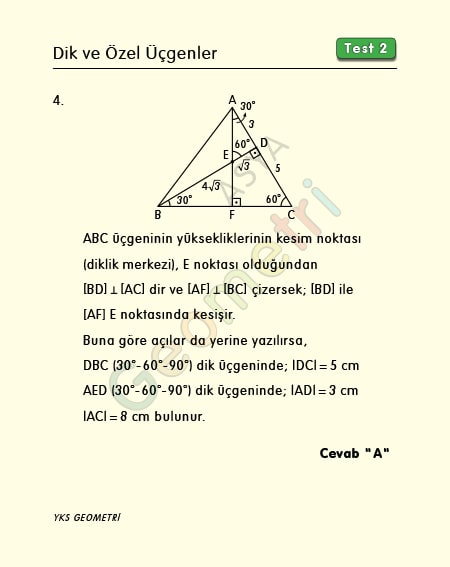
Problem 4’ün çözümü :

ABC üçgeninde E noktası diklik merkezi ise [BD], [AC] ye diktir. A köşesinden E noktasından geçecek şekilde bir doğru çizersek E diklik merkezi olduğundan [BC] yi dik kesecektir. 30 60 90 üçgenlerinden |AC|=8 cm bulunur.

Problem 5’in çözümü :

ABC dik üçgeninde [BD] kenarortay olduğundan |BC|=20 cm dir. ABC 15 75 90 üçgeni olduğundan hipotenüse ait yükseklik hipotenüsün dörtte biri olduğundan yükseklik=x=5 cm olur. (ispatlı)

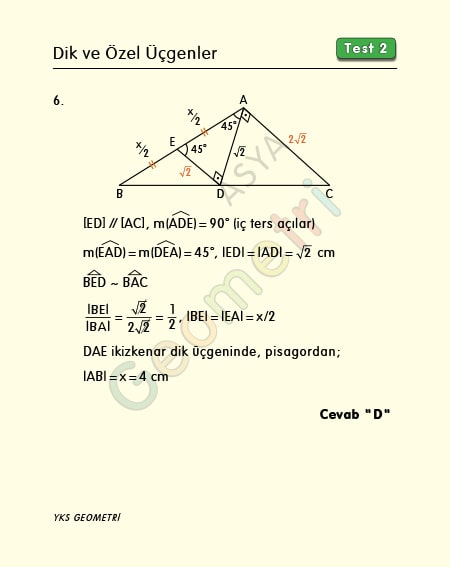
Problem 6’nın çözümü :

ABC üçgeninde D noktasından AB ye paralel çizelim. AED üçgeni ikizkenar dik üçgeni olacağından AD √2 olur ki oluşan benzer üçgenlerden DE uzunluğu ABD üçgenin kenarortaydır. AE uzunluğu 2 cm olduğundan AB uzunluğu 4 cm bulunur.

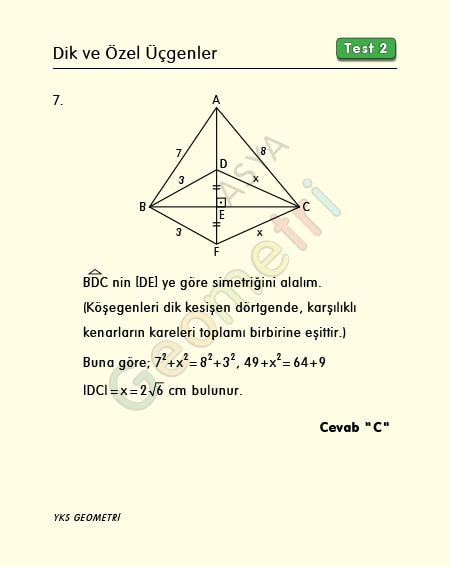
Problem 7’nin çözümü :

ABC üçgenindeki BDC üçgeninin simetriğini alırsak köşegenleri dik kesişen bir ABFC dörtgeni oluşur ki 7²+x²= 8²+3² olur. Buradan, x=2√6 bulunur. (ispatlı)

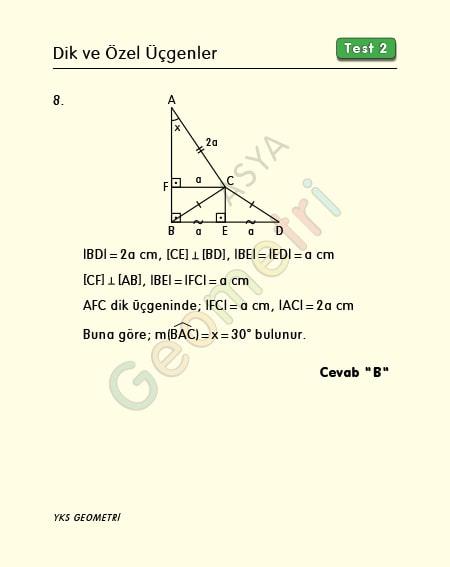
Problem 8’in çözümü :

İkizkenar üçgende tabana ait yükseklik aynı zamanda kenarortaydır. |BE|=|ED|=a cm dersek FBEC dikdörtgeninden, |BE|=|FC|=a cm olur. AFC dik üçgeninde hipotenüs |FC| nin iki katı olduğundan x açısının ölçüsü 30° bulunur.

Dik ve Özel Üçgenler test-2 PDF

Ders Geometri, ücretsiz olarak indirilebilen PDF formatında Dik ve Özel Üçgenler Test-2 PDF dosyasını sunar. Matematik alanında önemli bir yere sahip olan geometri dersi, öğrencilerimizin becerilerini güçlendirmek adına oldukça önemlidir. Bundan dolayı Ders Geometri ekibi, öğrencilerin geometri konularındaki yeteneklerini artırmak için özel olarak hazırlanmış testler sunmaktadır. Bu değerli içerik, ücretsiz olarak temin edilebilen PDF formatındadır.

Üçgen Testleri öğrencilere problem çözme becerilerini geliştirme fırsatı sağlamakta olup, özellikle üniversite giriş sınavları TYT ve AYT’ye hazırlanan öğrenciler için büyük bir destektir. Bu kaynak, geometri alanındaki anlayışı pekiştirmek ve sınav hazırlıklarını daha etkili hale getirmek isteyen her öğrencinin başvurabileceği değerli bir rehberdir.